


Next: Discussion 1: Learning Mathematics
Multivariable Calculus:
Collaborative Learning Workbook
David B. Damiano
Margaret N. Freije
Copyright © by Brooks/Cole Publishing Company
Contents
- Maple for Multivariable Calculus: A Summary of Useful Commands
- xvii
- Chapter 1: Euclidean Space and Vectors
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 1: Functions of Several Variables
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 2: The Coordinate System in
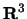
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 3: Using the Language of Vectors
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 4: The Geometry of Lines and Planes
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 5: Introduction to Optics
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Chapter 2: Parametric Curves and Vector Fields
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 6: Parametric Curves
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 7: Plotting Parametric Curves Using Maple
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 8: Further Exploration of Parametric Curves
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 9: The Derivative of a Parametrization
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 10: Applications of Parametric Curves
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 11: Vector Fields
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 12: Critical Points of Vector Fields
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 13: Vector Fields as Models
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 13A: Physical Models
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 13B: Models of Interacting Populations
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 13C: Epidemic Models
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Chapter 3: Differentiation of Real-Valued Functions
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 14: Contour Plots
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 15: Plotting Functions of Two Variables in Maple
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 16: Rates of Change
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 17: Local Linearity of Functions of Two Variables
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 18: Solving Systems of Equations
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Chapter 4: Critical Points and Optimization
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 19: Critical Points
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 20: Using Maple to Find Critical Points
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 21: The Second Derivative Test
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 22: Constrained Optimization
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 23: Lagrange Multipliers
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Chapter 5: Integration
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 24: Total Accumulation
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 25: Iterated Integrals in the Plane
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 26: Integration in Polar Coordinates
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 27: Iterated Integrals in Space
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Chapter 6: Integration on Curves
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 28: Riemann Sums on Paths in Space
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 29: Path Independence
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
- Discussion 30: Green's Theorem
-
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
startsection section10mm-.5 Chapter 1: Euclidean Space and Vectors
This chapter begins by developing the Euclidean coordinate system in
the plane and in space. The emphasis is on using the formal language
of mathematics, set notation, to describe subsets of the plane and
space as well as giving prose descriptions of these subsets. Sections
1.2 and 1.3 introduce vectors and vector algebra. In these sections
the language of vectors is used as another way to describe subsets of
the plane and space and to express other geometric concepts. Both
vectors themselves and the vector operations are discussed
symbolically and graphically. Thus a vector can be represented by an
ordered pair or triple, or by an arrow in the plane or in space. The
dot product is defined symbolically by the standard formula and then
interpreted geometrically in terms of the angle between two vectors.
Finally in Section 1.4, we use the language of Euclidean coordinates
and vectors to describe lines and planes in space. This chapter also
introduces several examples of the types of problems from the sciences
which will be used in the text. The emphasis is on using mathematical
language to describe these different phenomena.
The first five discussionss in this chapter are in-class discussions
and do not require access to the computer. Students should be able to
complete most of the work on each of these discussions in one class
period, although they may need time outside of class to complete a
write-up of their results. Discussion 6 is an extended assignment
which explores an application of the language of vectors to optics.
This discussion can be assigned as an out-of-class collaborative
exercise or it can be begun in class and then be completed outside of
class.
The following is a daily schedule for Chapter 1 incorporating discussions,
lectures and reading assignments.
- Day 1
- Discussion 1: Learning Mathematics or Discussion
2: Functions of Several Variables in class. Read Section 1.1:
Euclidean Coordinates for homework.
- Day 2
- A brief lecture on Section 1.1 emphasizing set
notation, followed by Discussion 3: The Coordinate System in
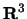 in class.
in class.
- Day 3
- A lecture on Section 1.2: Vectors emphasizing the
correpondence between points and vectors. Read Section 1.2 for
homework.
- Day 4
- Discussion 4: Using the Language of Vectors in
class, followed by a summary of students' results. Read Section 1.3:
Vector Products for homework.
- Day 5
- A lecture on Section 1.3.
- Day 6
- Finish Section 1.3, lecture on lines in the
plane and in space.
- Day 7
- Discussion 5: Planes in class. Read Section
1.4: Lines and Planes for homework.
- Day 8
- Finish chapter with lecture on planes in space. Assign
Discussion 6: Introduction to Optics as an extended exercise.
A brief description of each discussion including a statement of the
goals of the discussion, a synopsis of the discussion, suggested
reading assignments and an indication of which questions or models
will be used again in subsequent discussions is given below.



Next: Discussion 1: Learning Mathematics
2000-08-31
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif)