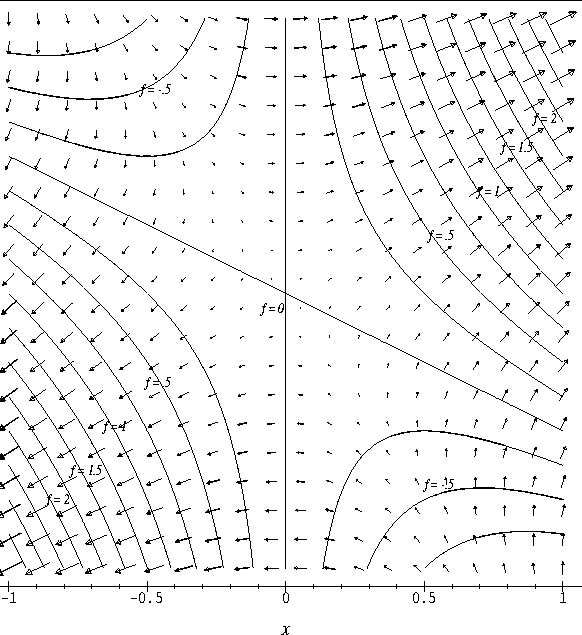
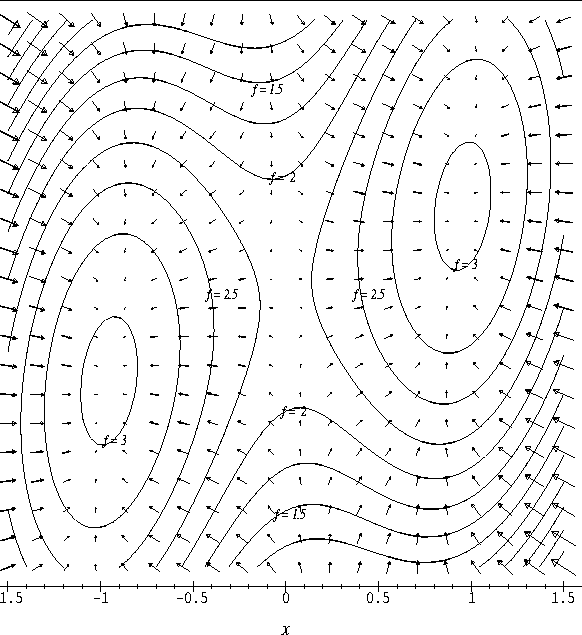
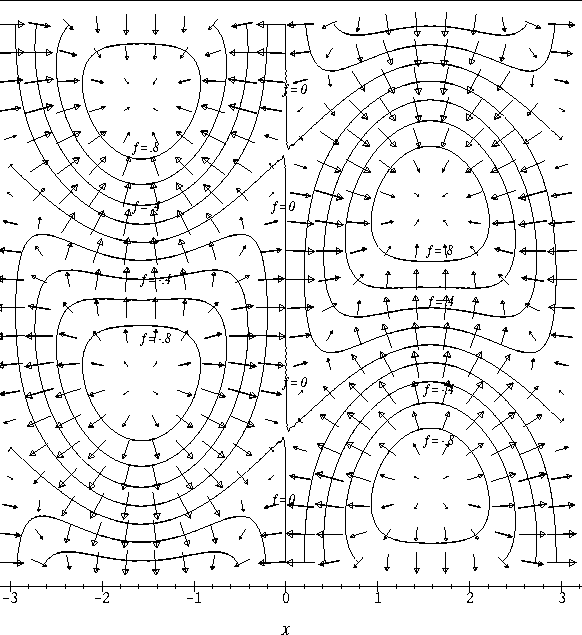
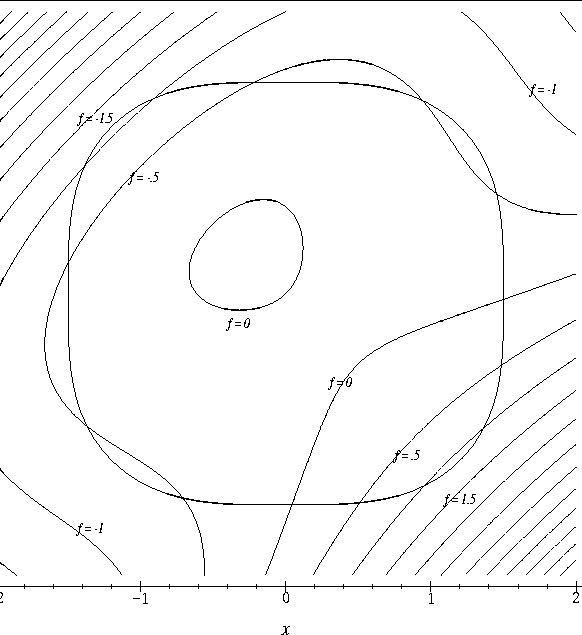
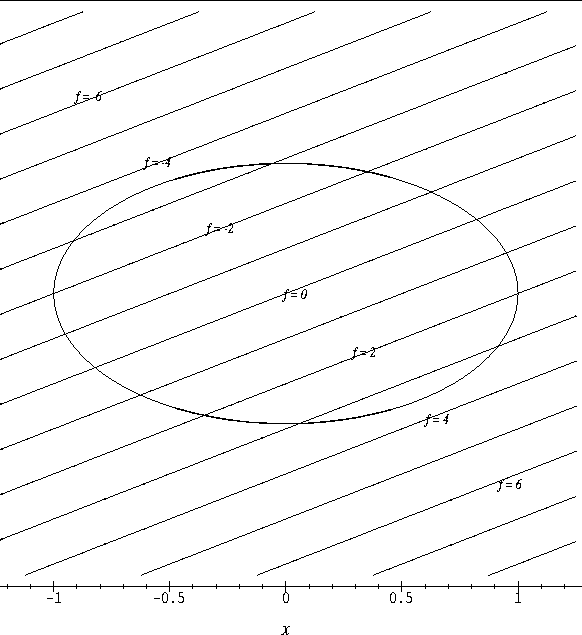
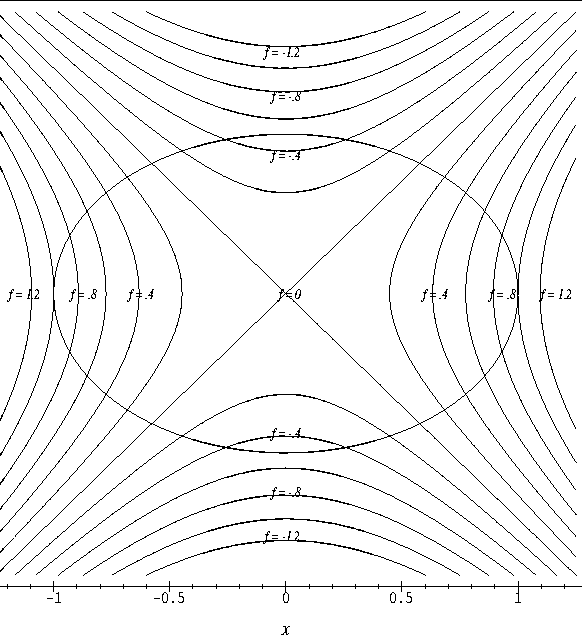
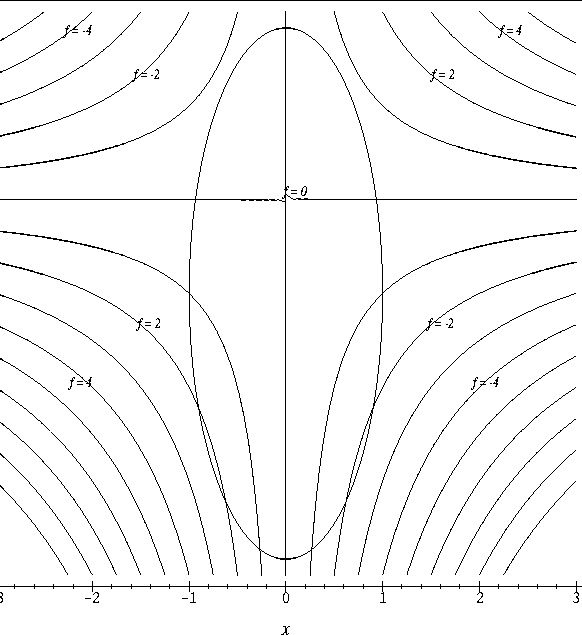
We have already seen in class that we can classify these critical points as relative maxima, relative minima or saddle points by considering the contour plot of f in an open set containing the critical point. In this discussion we will develop another graphical technique for classifying the critical points of f.
Recall that if f is a differentiable function defined on the open set
![]() , the gradient vector of f,
, the gradient vector of f,
![]() is defined at every point
is defined at every point
![]() . Thus we can define
a vector field on
. Thus we can define
a vector field on ![]() , called the gradient vector field
of f, whose coordinate functions are the first partial derivatives
of f. That is,
, called the gradient vector field
of f, whose coordinate functions are the first partial derivatives
of f. That is,
for any
The goal in this discussion is to use a classification of the critical
points of the vector field ![]() to determine a classification of
critical points of f.
to determine a classification of
critical points of f.
startsection subsection10mm.5 Exercises
- 1.
- Attached to this discussion you will find plots of the vector
field
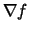 displayed on the contour plot of f for three
different functions f. On each plot,
displayed on the contour plot of f for three
different functions f. On each plot,
- (a)
- locate the critical points of the vector field,
- (b)
- sketch several flow lines of the vector field, and
- (c)
- classify the critical points of the vector field.
- 2.
- Based on the plots of
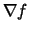 and the contours of f that
you considered in Exercise 1, and your knowledge of the gradient
vector, what is the relationship between the flow lines of f and the
contours of f? What happens to the values of f as you move along a flow line?
and the contours of f that
you considered in Exercise 1, and your knowledge of the gradient
vector, what is the relationship between the flow lines of f and the
contours of f? What happens to the values of f as you move along a flow line?
- 3.
- We determined in our analysis of vector fields that there are
four different types of critical points: sinks, sources, saddles and
centers. We've seen that the critical points of a function f can be
classified as maxima, minima or saddle points. Explain how you would
use the classification of critical points of the vector field,
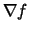 to classify the critical points of the function f. Based upon
the correspondence you have established between the types of critical
points of
to classify the critical points of the function f. Based upon
the correspondence you have established between the types of critical
points of 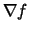 and the types of critical points of f, are
there any types of critical points for vector fields which you would
not expect to find as critical points of gradient vector fields?
and the types of critical points of f, are
there any types of critical points for vector fields which you would
not expect to find as critical points of gradient vector fields?
startsection section10mm-.5 Discussion 24 Using Maple to Find Critical Points
This is a LATEXversion of a Maple worksheet. The worksheet is available in the directory
/home/stu/courses/math141.
startsection subsection10mm.5 Introduction
In this discussion we would like to use both the graphical and numerical capabilities of Maple to locate and identify critical points of functions of two variables.
As we have seen in the text, a critical point of a differentiable
function
f = f(x,y) of two variables is a point for which the gradient
vector is equal to zero. That is, (x,y) satsifies:
This is equivalent to the following system of equations in two unknowns:
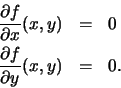
In Discussion
fsolve, which utilizes a modified form of the
Newton-Raphson method. Unlike newrap, fsolve does not
give the user control of the number of iterates used to produce the
solution. In the following example, we will see how to use fsolve and the built-in Maple plotting commands.
startsection subsection10mm.5 An Example
Let us use the Maple plotting commands and fsolve to find and identify
the critical points of the function.
f:=(x,y)-> y^3 - 2*y -5 - 3*x^2;
In order to make a preliminary guess about the number of critical
points, let us examine a contour plot of f. Note that we are
confining our attention to the rectangle
contourplot(f(x,y),x=-2..2,y=-2..2);
Based upon the plot, we expect that f has a critical point located
at approximately (0,-.8) that is a maximum or minimum and a critical
point located at approximately (0, .8). In order to obtain a more
accurate approximation, we can employ fsolve. The fsolve
command will solve a system of equations for several variables in a
specific region. A convenient way to do this is first define the set
of equations and then define the set of variables. Notice that we are
using the operator D to compute the partial derivatives of f.
For example, D[1](f) is the partial derivative of f with
respect to the first variable in the definition of f, which is xin this case.
eqns:={D[1](f)(x,y) = 0, D[2](f)(x,y)=0};
vars:={x,y};
The following use of fsolve does not specify a region. Let us see what happens:
fsolve(eqns,vars);
This returns a single critical point that is approximately located at (0,-.8165). (Note that the full value to 10 decimal places is still only an approximation to a solution.) Apparently, this is the critical point that we located at (0,-.8). To find the other critical point, let us specify a domain.
fsolve(eqns,vars,y=0..1);
This yields the other critical point which is approximately located at
(0, .8165). Note that if the region is left unspecified, the
numerical values generated by fsolve may fail to converge. To remedy
this problem, you must specify a region.
To identify the type of these critical points, we might use
contourplot, but display more contours and focus our attention on region containing a critical point:
contourplot(f(x,y),x=-.5 .. .5,y=.5.. 1.5,contours=25);
We see that the contours appear to form a family of hyperbolas, which
indicates that the critical point is a saddle. We might also plot the
graph of the function on the same region.
plot3d(f(x,y),x=-.5.. .5, y= .5 .. 1.5,axes = BOXED,
style=PATCHCONTOUR,view=-6.4..-5);
Notice in the preceding plot3d command we specified several options.
We chose the axes to appear as the frame of a box; we chose the plot
to be shaded and to display horizontal slices, and we restricted the
vertical portion of the plot to the interval [-6.4,-5]. This last
option is particularly useful since it can eliminate portions of the
graph whose z-values are not close to the value at the critical point.
In a similar manner we could examine the behavior of f in a region containing the other critical point. We would find that it is a local maximum.
In this case, it is apparent from the equations that f has no other critical points, so we are done.
startsection subsection10mm.5 Exercises
For each of the following functions, use Maple to locate and identify
all the critical points. As above, you should use the contour plot to
determine the approximate location of the critical points and then use
fsolve to locate them more precisely. If you find that a critical
point is difficult to locate or identify, explain why the behavior of
the function made it difficult to locate.
Before starting the exercises be sure to load the plots package:
with(plots):
When working with a new function, enter the following definitions after defining
the function and before using fsolve.
eqns:={D[1](f)(x,y) = 0, D[2](f)(x,y)=0}:
vars:={x,y}:
When working with a new function, enter the following definitions.
- 1.
f:=(x,y)-> -x^2*(x^2 - 4) + y^4 + x^2 + y^2:- 2.
- This function is expressed in terms of the hyperbolic secant functions, sech, which is
defined by
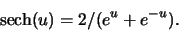
f:=(x,y)-> sech((x+.5)^2 + y^2) + 2*sech((x-1)^2 + (y-2)^2):
- 3.
f:=(x,y)->1/(1 + x^2 + (y-1)^2) - 2/(1 +(x-1)^2 + (y-x)^2);
startsection section10mm-.5 Discussion 25 The Second Derivative Test
In this discussion we will apply the second derivative test to two
functions. First, let us review the hypothesis of the second
derivative test. We must have that f is a twice
differentiable function of two variables and that (x0,y0) is a
critical point of f, that is,
![]() . Let
. Let
If
startsection subsection10mm.5 Exercises For each of the following functions
(i) Compute the partial derivativesand
.
(ii) Find the critical points of f.
(iii) Compute the second partial derivatives of f.
(iv) Use the second derivative test to classify the non-degenerate critical points of f.
(v) If there are any degenerate critical points, use another method to determine if these critical points are local maxima, local minima or saddle points.
- 1.
- f(x,y) = x3 - 6xy + y3.
- 2.
-
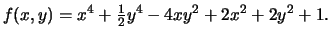
startsection section10mm-.5 Discussion 26 Constrained Optimization
We have so far developed geometric and symbolic methods to locate and
classify relative extrema of a differentiable function f on an open set in ![]() . In this discussion, we want to extend
these techniques so that we can locate extrema on a closed set
. In this discussion, we want to extend
these techniques so that we can locate extrema on a closed set ![]() consisting of
an open set
consisting of
an open set ![]() and its boundary curve
and its boundary curve ![]() . The extrema for f on
. The extrema for f on ![]() must occur at either the relative extrema of f on
must occur at either the relative extrema of f on ![]() or at the relative extrema of f on
or at the relative extrema of f on ![]() . Since we already
have techniques for finding relative extrema on
. Since we already
have techniques for finding relative extrema on ![]() , we need
only develop a technique for locating relative extrema on
, we need
only develop a technique for locating relative extrema on ![]() .
Here we will consider the case where
.
Here we will consider the case where ![]() , the boundary of
, the boundary of
![]() , is a set of points satisfying an equation of the form
g(x,y) = c, where g is a differentiable function. We will call a
condition of this type a constraint and speak of optimizing fsubject to a constraint.
, is a set of points satisfying an equation of the form
g(x,y) = c, where g is a differentiable function. We will call a
condition of this type a constraint and speak of optimizing fsubject to a constraint.
In this discussion we will approach the problem of locating the extrema of f subject to the constraint g(x,y) = c by considering the relationship between the level sets of f and the curve g(x,y) = c. Our aim is to give a graphical characterization of the extreme points of f on this boundary curve, and to use this to produce a symbolic characterization that will lead to a symbolic solution of the problem.
startsection subsection10mm.5 Exercises
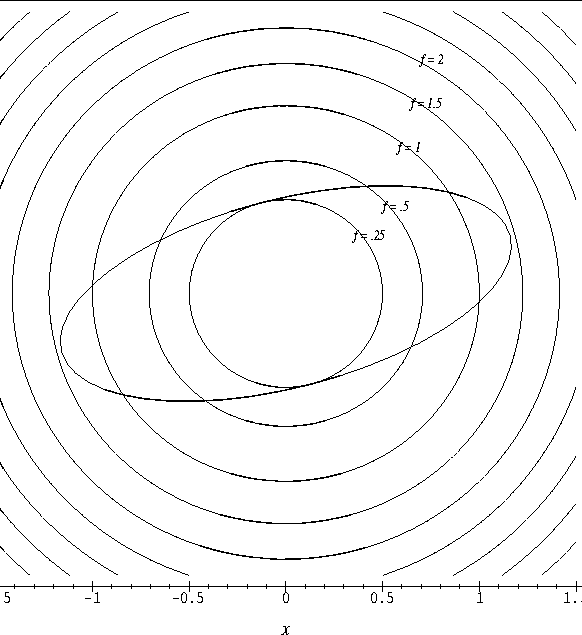
- 1.
- Attached to this discussion are plots for three constrained
optimization problems. Each plot consists of the contours of a
differentiable function f and the boundary curve g(x,y) =c.
- (a)
- For each plot, use the values assigned to the contours to locate
the maximum and minimum values of f on the boundary curve.
- (b)
- What is the relationship between the contour curve of f and the
boundary curve at the extreme points?
- (c)
- We have seen that the vector field
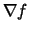 can provide
information for analyzing extreme values of f. For each plot,
sketch
can provide
information for analyzing extreme values of f. For each plot,
sketch 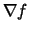 on the contour plot. What is the relationship
between
on the contour plot. What is the relationship
between 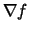 and the boundary curve at the extreme points of
f on the boundary curve?
and the boundary curve at the extreme points of
f on the boundary curve?
- (d)
- The boundary curve
g(x,y) = c is a level set for the
differentiable function g. What does this imply about the
relationship between
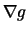 and the boundary curve?
and the boundary curve?
- (e)
- What is the relationship between
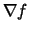 and
and 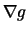 at the
extreme points of f on the boundary curve?
at the
extreme points of f on the boundary curve?
- 2.
- (a)
- Use your graphical characterization from Exercise 1 to produce a
symbolic characterization of the extreme points of f subject to the constraint
g(x,y) = c.
- (b)
- How would you use this symbolic characterization to algebraically
solve for the extreme points of f subject to the constraint
g(x,y) =
c.
- 3.
- Consider the three plots again.
- (a)
- Are there other points on the boundary curve which would satisfy
the graphical conditions you summarized in Exercise 1? Locate these points.
- (b)
- What is the behavior of f on the boundary curve at these points?
startsection section10mm-.5 Discussion 27 Lagrange Multipliers
In this discussion we will work through examples of finding the
extreme values of a function on a closed set
![]() . Let f be a differentiable function defined on an open set containing
. Let f be a differentiable function defined on an open set containing ![]() . We will locate the critical points of f on
. We will locate the critical points of f on ![]() ,
the interior of
,
the interior of ![]() by solving the equation
by solving the equation
![]() .
We will then use the method of Lagrange multipliers to locate the
extreme values of f on the boundary
.
We will then use the method of Lagrange multipliers to locate the
extreme values of f on the boundary ![]() . Let us recall the
statement of the method.
. Let us recall the
statement of the method.
Assume ![]() is described by the equation
g(x,y) = c, where g is a differentiable
function and
is described by the equation
g(x,y) = c, where g is a differentiable
function and
![]() on
on ![]() .
Then the extreme values of f on
.
Then the extreme values of f on ![]() occur at
solutions to the system of equations
occur at
solutions to the system of equations
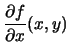 |
= | 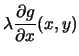 |
|
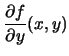 |
= | 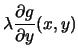 |
|
| g(x,y) | = | c. |
Recall that not all the points that are critical points in
startsection subsection10mm.5 Exercises
Attached to the discussion sheet are plots for the following three
constrained optimization problems. Each plot consists of the contours
of a function f and the curve which is the boundary of ![]() .
For each of these problems, locate the critical points of f on
.
For each of these problems, locate the critical points of f on
![]() , the interior of the closed set
, the interior of the closed set ![]() , on the plot and
then solve the equation
, on the plot and
then solve the equation
![]() to determine these
points symbolically. Then use the plot to locate the relative and
absolute extreme points of f on the boundary curve and write out and
solve the Lagrange multiplier system of equations in order to find the
coordinates of the extreme points of f subject to the constraint.
Keep in mind that while you cannot find exact values for the
coordinates of the extreme points from the contour plot, you can use
the plot to determine the number and type of the extreme points.
to determine these
points symbolically. Then use the plot to locate the relative and
absolute extreme points of f on the boundary curve and write out and
solve the Lagrange multiplier system of equations in order to find the
coordinates of the extreme points of f subject to the constraint.
Keep in mind that while you cannot find exact values for the
coordinates of the extreme points from the contour plot, you can use
the plot to determine the number and type of the extreme points.
- 1.
- Find the extreme values of
f(x,y) = 2x - 5y on the closed set
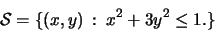
(See Figure![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .)
.)
- 2.
- Find the extreme values of
f(x,y) = x2 - y2 on the closed set
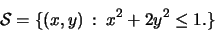
(See Figure![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .)
.)
- 3.
- Find the extreme values of
f(x,y) = xy -x on the closed set
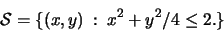
(See Figure![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .)
.)
Next: Integration Up: Multivariable Calculus: Collaborative Learning Previous: The Sequence of Approximations
2000-08-31