


Next: Integration on Curves
Up: Multivariable Calculus: Collaborative Learning
Previous: Optimization
Integration
startsection section10mm-.5 Discussion 28 Total Accumulation
In this discussion we want to develop a method for approximating the
total accumulation of a function of two variables. The
particular function that we will be using is ``daily snowfall'' and
the total accumulation will be the total volume of snowfall.
On March 12-15, 1993, the so-called ``Storm of the Century'' hit the
east coast of the United States. Snowfall totals over 50 inches were
recorded in some areas of Tennessee and North Carolina with drifts of
over 14 feet. The National Weather Service's Office of Hydrology
estimated the volume of water that fell as snow as 44 million
acre-feet, which is comparable to 40 days' flow on the Mississippi
River at New Orleans. (An acre-foot is the amount of water it would
take to cover one acre to a depth of one foot.) In this discussion,
using data and a plot from the National Climatic Data Center, we would
like to determine the volume of water in the form of snow that fell on
one region--New Jersey, New York (excluding Long Island), and
Pennsylvania--on one day of this storm. The ratio of snow depth to
water depth was approximately 5:1, so that 5 inches of snow is
equivalent to 1 inch of rain. Thus the total volume of water that
fell will be 1/5 the total volume of snow that fell.
startsection subsection10mm.5 Exercises
Figure ![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) contains the snowfall data for March 13, 1993
for New Jersey, New York, and Pennsylvania. The locations of the data
collection sites are given in latitude and longitude and the snowfall
measurements are given in tenths of inches. The locations are marked
on the density plot in Figure
contains the snowfall data for March 13, 1993
for New Jersey, New York, and Pennsylvania. The locations of the data
collection sites are given in latitude and longitude and the snowfall
measurements are given in tenths of inches. The locations are marked
on the density plot in Figure ![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) . The plot is shaded
according to the accompanying key to indicate snowfall amounts for
March 13, 1993, for the eastern United States. Note: There are 640
acres in a square mile, one degree of latitude is approximately 69
miles, and one degree of longitude (in this region) is approximately
51 miles. Your numerical answers should be given in square mile-feet of snow.
. The plot is shaded
according to the accompanying key to indicate snowfall amounts for
March 13, 1993, for the eastern United States. Note: There are 640
acres in a square mile, one degree of latitude is approximately 69
miles, and one degree of longitude (in this region) is approximately
51 miles. Your numerical answers should be given in square mile-feet of snow.
- 1.
- (a)
- Given a region of the plot in Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) what
method would you use to approximate the total volume of snow that
fell on the region?
what
method would you use to approximate the total volume of snow that
fell on the region?
- (b)
- Use your method to produce a value that approximates the total
volume of snow that fell on New Jersey, New York (excluding Long
Island), and Pennsylvania.
- 2.
- (a)
- How would you improve upon your method to produce a better
approximation to the total volume of snow? Explain why this would
produce a better approximation to the total volume of snow.
- (b)
- Based upon your answer to Exercise 2(a), improve upon the
approximation that you produced in Exercise 1(b).
- 3.
- Can your method be used to produce an exact value for the total
volume of snow represented by the plot? If so, explain how this might
be done. In particular, what, if any, additional information about
the snowfall function would you need to know in order to produce an
exact value by this method.
Figure:
Data for snowfall in the New Jersey, New York, and
Pennsylvania on March 13, 1993, from the ``Storm of the Century''.
The amount of snow is given as a function of latitude and longitude
and is given in tenths of inches. Note that west longitude is
written as a negative number. (Data is courtesy of the National
Climatic Data Center.)
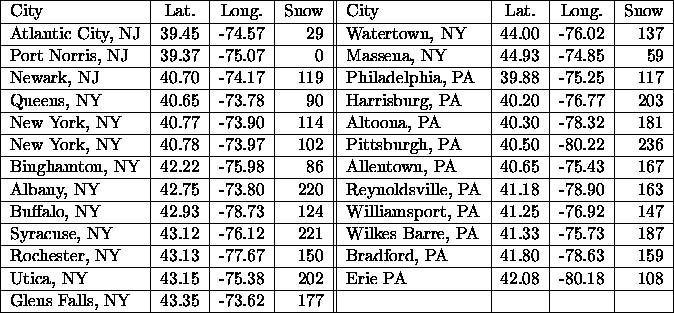 |
Figure:
 |
startsection section10mm-.5 Discussion 29 Iterated Integrals in the Plane
In this discussion we would like to focus on the connection between
partitions of a region
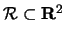 and the iterated integral
representation of a double integral over
and the iterated integral
representation of a double integral over  , which is given by
Fubini's theorem (see Section 5.2 of the text). Let us first review
this connection.
, which is given by
Fubini's theorem (see Section 5.2 of the text). Let us first review
this connection.
Suppose that  is defined by the inequalities
is defined by the inequalities
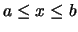 and
and
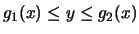 , where g1 and g2
are continuous functions of one variable. In order to partition
, where g1 and g2
are continuous functions of one variable. In order to partition
 into
into 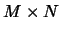 rectangular cells, we first partitioned
rectangular cells, we first partitioned  into
M columns of width
into
M columns of width
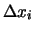 ,
,
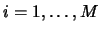 , and then
partitioned the ith column into N cells of height
, and then
partitioned the ith column into N cells of height
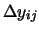 . (See Figure
. (See Figure ![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .) This led to a
Riemann sum for the total accumulation of f which could be written
as an iterated sum,
.) This led to a
Riemann sum for the total accumulation of f which could be written
as an iterated sum,
where we sampled f in the ijth cell at
(xi*,
yij*). The limit of Riemann sums of this form is the iterated
integral
The order of evaluation of the iterated integral, first y and then
x, is determined by the form of the Riemann sum, which is in turn
determined by the geometry of  .
.
Figure:
(a) A region defined by
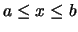 and
and
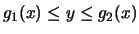 partitioned into M=6 columns with N=5 cells in
each column. The second cell in the third column, which has
dimensions
partitioned into M=6 columns with N=5 cells in
each column. The second cell in the third column, which has
dimensions
 ,
is shaded. (b) A
region defined by
,
is shaded. (b) A
region defined by
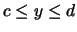 and
and
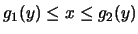 partitioned into N=5 rows with M=3 cells in each row. The second
cell in the second row, which has dimensions
partitioned into N=5 rows with M=3 cells in each row. The second
cell in the second row, which has dimensions
 ,
is shaded.
,
is shaded.
![\begin{figure}
\centering
\subfigure[]{\psfig{file=chapter5d/betweengraphs1.ps,h...
...=chapter5d/betweengraphs2.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img269.gif) |
If the roles of x and y are reversed, and  is defined by
inequalities
is defined by
inequalities
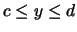 and
and
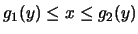 ,
then we would first partition
,
then we would first partition  into N rows, and then partition
each row into M cells. (See Figure
into N rows, and then partition
each row into M cells. (See Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .) After writing out the corresponding
iterated sum form for the Riemann sum and evaluating the limit of
Riemann sums, we arrived at the following iterated integral,
.) After writing out the corresponding
iterated sum form for the Riemann sum and evaluating the limit of
Riemann sums, we arrived at the following iterated integral,
Here we integrate first with respect to x and then with respect to y.
To summarize: when  lies between vertical lines x=a and x=b,
we first partitioned
lies between vertical lines x=a and x=b,
we first partitioned  into columns and then partitioned the
columns, which ultimately gives an iterated integral first with
respect to y and then with respect to x; and when
into columns and then partitioned the
columns, which ultimately gives an iterated integral first with
respect to y and then with respect to x; and when  lies
between horizontal lines y = c and y = d, we first partitioned
lies
between horizontal lines y = c and y = d, we first partitioned  into rows and then partitioned the rows, which gives an iterated
integral first with respect to x and then with respect to y.
into rows and then partitioned the rows, which gives an iterated
integral first with respect to x and then with respect to y.
startsection subsection10mm.5 Exercises
- 1.
- (a)
- For each of the regions in Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) , sketch a
partition of the region consisting of
, sketch a
partition of the region consisting of
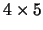 rectangular cells
organized either into columns or into rows. Explain your choice.
rectangular cells
organized either into columns or into rows. Explain your choice.
- (b)
- Set up the iterated integral of a function f=f(x,y) over the
regions of Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) corresponding to your partitions
in part (a).
corresponding to your partitions
in part (a).
- 2.
- For each of the following regions
 ,
(i) Sketch
,
(i) Sketch  and a
partition of
and a
partition of  into rectangular cells organized either into
columns or into rows. Be sure to label the boundary curves of
into rectangular cells organized either into
columns or into rows. Be sure to label the boundary curves of  .
(ii) Set up the iterated integral of a function f over
.
(ii) Set up the iterated integral of a function f over  corresponding to your partition.
corresponding to your partition.
- (a)
-
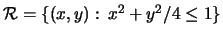 .
.
- (b)
-
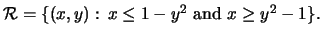
- (c)
-
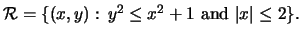
- 3.
- For each of the regions in Exercises 1 and 2, if possible,
describe the region so that the roles of x and y are reversed from
the original description, sketch a partition of the region into
columns of equal width or rows of equal height corresponding to the
new description, and give the corresponding iterated integral. If this
is not possible, explain why not.
startsection section10mm-.5 Discussion 30 Integration in Polar Coordinates
This discussion provides an opportunity to work through several
examples of integration in the plane using polar coordinates and to
think about the examples where it is necessary to choose an
appropriate coordinate system before carrying out an integration.
coordinates.
startsection subsection10mm.5 Exercises
- 1.
- Let
 be the region in the first quadrant of the
xy-plane that lies between the circle of radius 1 centered at the
origin and the circle of radius 2 centered at the origin. Let
be the region in the first quadrant of the
xy-plane that lies between the circle of radius 1 centered at the
origin and the circle of radius 2 centered at the origin. Let 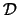 be the region in the first octant of space lying over
be the region in the first octant of space lying over  and under the graph of the function
f(x,y) = 8 - x2 -y2.
and under the graph of the function
f(x,y) = 8 - x2 -y2.
- (a)
- Sketch the region
 and a partition of
and a partition of  into
polar rectangles.
into
polar rectangles.
- (b)
- Set up and evaluate a polar integral for the volume of the
region
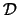 .
.
- 2.
- A plane carrying a load of 500 killer bees has conveniently crashed
at the origin in the xy-plane. Over time, the bees spread out from
the origin in a random manner so that the concentration of bees per
square mile can be modelled by a function c of x, y, and t,
Here t=0 corresponds to the time of the crash. Fixing t,
c(x,y,t) represents the concentration of bees per square mile at
time t at the point (x,y). We are interested in finding the
number of bees that remain within one mile from the origin after 1/2
hour.
- (a)
- Sketch a partition of the region
 consisting of
points of distance less than or equal to 1 from the origin. Use
consisting of
points of distance less than or equal to 1 from the origin. Use
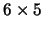 polar rectangles.
polar rectangles.
- (b)
- Set up and evaluate a polar integral for the total number of
bees that remain inside the area consisting of points of distance
less than or equal to 1 mile from the origin after 1/2 hour.
- 3.
- For each of the regions
 and functions f, (i) sketch
the region
and functions f, (i) sketch
the region  ,
(ii) partition
,
(ii) partition  using either
rectangular or polar coordinates, (iii) set up and evaluate an
integral for the total accumulation of f on
using either
rectangular or polar coordinates, (iii) set up and evaluate an
integral for the total accumulation of f on  corresponding
to your choice of partition of
corresponding
to your choice of partition of  .
.
- (a)
 is the set of points (x,y) in the first quadrant of
the xy-plane satisfying
is the set of points (x,y) in the first quadrant of
the xy-plane satisfying 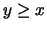 and
and
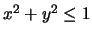 .
f(x,y) = y.
.
f(x,y) = y.
- (b)
-
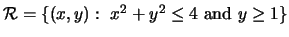 .
f(x,y) = x2 y.
.
f(x,y) = x2 y.
- (c)
-
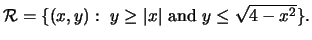 f(x,y) = x.
f(x,y) = x.
startsection section10mm-.5 Discussion 31 Iterated Integrals in Space
In this discussion we would like to focus on the connection between
partitions of a region
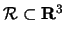 and the iterated integral
representation of the integral of a function over
and the iterated integral
representation of the integral of a function over  . As was the
case in the plane, this is given by Fubini's theorem. In particular,
we would like to introduce an intuitive way to think about this
connection in terms of sampling schemes. Let us work with a region
. As was the
case in the plane, this is given by Fubini's theorem. In particular,
we would like to introduce an intuitive way to think about this
connection in terms of sampling schemes. Let us work with a region
 defined by
defined by
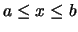 ,
,
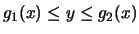 ,
and
,
and
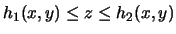 , where g1, g2, h1 and
h2 are continuous functions.
, where g1, g2, h1 and
h2 are continuous functions.
In order to construct a Riemann sum for the total accumulation of fon  , we will sample the value of f by inserting ``sensors'' on
``wires'' into
, we will sample the value of f by inserting ``sensors'' on
``wires'' into  to record the values of f. For example, if
to record the values of f. For example, if
 represents a container of liquid and we want to find the total
heat of the liquid, we would insert
represents a container of liquid and we want to find the total
heat of the liquid, we would insert
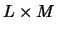 wires into the fluid
with N small temperature sensors on each wire to measure the
temperature in the container. Intuitively, we would insert the wires
parallel to the z-axis through the top of the container in a
rectangular pattern and the space the N sensors along the wires.
The pattern of the wires depends on the geometry of the projection
wires into the fluid
with N small temperature sensors on each wire to measure the
temperature in the container. Intuitively, we would insert the wires
parallel to the z-axis through the top of the container in a
rectangular pattern and the space the N sensors along the wires.
The pattern of the wires depends on the geometry of the projection
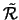 of the region in the xy-plane. We would partition
of the region in the xy-plane. We would partition
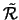 into
into 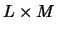 cells as we did in Discussion 25, and
then insert one wire into each cell. In this case,
cells as we did in Discussion 25, and
then insert one wire into each cell. In this case,
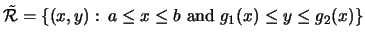 . (See Figure
. (See Figure ![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .) Since
.) Since
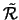 lies
between the graphs of functions of x, over an interval
lies
between the graphs of functions of x, over an interval
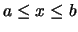 , we would partition
, we would partition
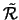 into L columns with Mcells in each column and then insert the
into L columns with Mcells in each column and then insert the
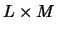 wires into the
cells of the partition of
wires into the
cells of the partition of
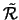 . The sensors should be placed
on the wires so that they are located above the graph of h1 and
below the graph of h2. This sampling scheme would
correspond to an iterated Riemann sum of the form
. The sensors should be placed
on the wires so that they are located above the graph of h1 and
below the graph of h2. This sampling scheme would
correspond to an iterated Riemann sum of the form
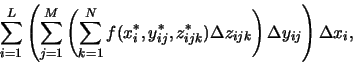
where
(xi*,yij*,zijk*) is the location of the ijkth
sensor and
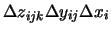 is
the volume of the three-dimensional cell containing this sensor. This
Riemann sum corresponds to the triple iterated integral
is
the volume of the three-dimensional cell containing this sensor. This
Riemann sum corresponds to the triple iterated integral
Notice that the direction of the wires, parallel to the z-axis,
corresponds to the inner or first variable of integration. This was
determined by our description of  as lying between the graphs of
two functions of x and y. The second and third variable of
integration correspond to the partition of
as lying between the graphs of
two functions of x and y. The second and third variable of
integration correspond to the partition of
 and are
determined by our description of
and are
determined by our description of
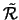 as lying between the
graphs of two functions of x, for
as lying between the
graphs of two functions of x, for
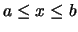 . .
. .
Figure:
(a) A region  defined by
defined by
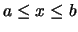 ,
,
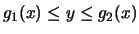 ,
and
,
and
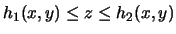 .
Here,
.
Here,
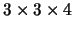 sensors are placed on
sensors are placed on
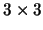 wires inserted into
wires inserted into  parallel
to the z-axis. Note the partition of
parallel
to the z-axis. Note the partition of  is not shown. (b) The
projection of
is not shown. (b) The
projection of  in the xy-plane is defined by
in the xy-plane is defined by
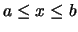 and
and
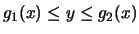 .
The wires in (a) are located at
the points
(xi,yij) in (b), which lie in the projections to the
xy-plane of the cells of the partition of
.
The wires in (a) are located at
the points
(xi,yij) in (b), which lie in the projections to the
xy-plane of the cells of the partition of  .
.
![\begin{figure}
\centering
\subfigure[]{\psfig{file=chapter5d/wires1.ps,height=2....
...fig{file=chapter5d/wires2.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img294.gif) |
If  had been described instead as lying between the graphs
of functions of y and z, we would have inserted the wires parallel
to the x-axis. The location of the wires would then be determined
by the description of the projection of
had been described instead as lying between the graphs
of functions of y and z, we would have inserted the wires parallel
to the x-axis. The location of the wires would then be determined
by the description of the projection of  in the yz-plane.
Similarly, if
in the yz-plane.
Similarly, if  had been described as lying between the graphs of
functions of y and z, we would have inserted the wires parallel to
the y-axis. The location of the wires would then be determined by
the description of the projection of
had been described as lying between the graphs of
functions of y and z, we would have inserted the wires parallel to
the y-axis. The location of the wires would then be determined by
the description of the projection of  in the xz-plane.
in the xz-plane.
Figure:
(a) The region
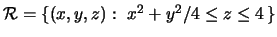 of Exercise 1. (b) The region
of Exercise 1. (b) The region
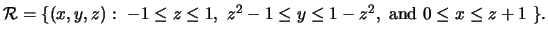 of
Exercise 2.
of
Exercise 2.
![\begin{figure}
\centering
\subfigure[]{\psfig{file=chapter5d/wireregions1.ps,hei...
...le=chapter5d/wireregions2.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img297.gif) |
startsection subsection10mm.5 Exercises
Each of these exercises refers to the intuitive process described
above for sampling a function f on a region  and writing
out a corresponding iterated integral.
and writing
out a corresponding iterated integral.
- 1.
- For the region
 in space described by
in space described by
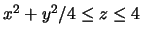 (see Figure
(see Figure ![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) ), describe the
projection of
), describe the
projection of  in the xy-plane, describe how to insert the wires
into
in the xy-plane, describe how to insert the wires
into  ,
describe the placement of the sensors on the wires, and
give the corresponding iterated integral.
,
describe the placement of the sensors on the wires, and
give the corresponding iterated integral.
- 2.
- For the region
 in space described by
in space described by
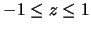 ,
,
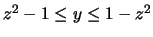 ,
and
,
and
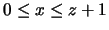 (see Figure
(see Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) ), choose an axis to use for the sampling process,
describe the projection of
), choose an axis to use for the sampling process,
describe the projection of  in the corresponding coordinate plane,
describe how to insert the wires into
in the corresponding coordinate plane,
describe how to insert the wires into  ,
describe the placement
of the sensors on the wires, and give the corresponding iterated
integral.
,
describe the placement
of the sensors on the wires, and give the corresponding iterated
integral.
- 3.
- For the region
 in space described by
in space described by
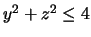 and
and
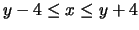 , choose an axis to use for the sampling
process, describe the projection of
, choose an axis to use for the sampling
process, describe the projection of  in the corresponding coordinate
plane, describe how to insert the wires into
in the corresponding coordinate
plane, describe how to insert the wires into  ,
describe the
placement of the sensors on the wires, and give the corresponding
iterated integral.
,
describe the
placement of the sensors on the wires, and give the corresponding
iterated integral.
- 4.
- According to our intuitive sampling scheme, we inserted wires in
 parallel to a coordinate axis in an arrangement of rows or an
arrangement of columns, depending on the description of the projection
of
parallel to a coordinate axis in an arrangement of rows or an
arrangement of columns, depending on the description of the projection
of  in the coordinate plane perpendicular to this axis. Let us
suppose that
in the coordinate plane perpendicular to this axis. Let us
suppose that  is the region lying between two functions of xand y and that the projections
is the region lying between two functions of xand y and that the projections
 of
of  in the
xy-plane is a disk of radius r0 centered at the origin. In this
case, ignoring the idea of columns or rows, how might you insert
in the
xy-plane is a disk of radius r0 centered at the origin. In this
case, ignoring the idea of columns or rows, how might you insert
 wires into
wires into  to take advantage of the geometry of
to take advantage of the geometry of
 ? Justify this arrangement and describe the resulting
arrangement of sensors.
? Justify this arrangement and describe the resulting
arrangement of sensors.



Next: Integration on Curves
Up: Multivariable Calculus: Collaborative Learning
Previous: Optimization
2000-08-31
![]() contains the snowfall data for March 13, 1993
for New Jersey, New York, and Pennsylvania. The locations of the data
collection sites are given in latitude and longitude and the snowfall
measurements are given in tenths of inches. The locations are marked
on the density plot in Figure
contains the snowfall data for March 13, 1993
for New Jersey, New York, and Pennsylvania. The locations of the data
collection sites are given in latitude and longitude and the snowfall
measurements are given in tenths of inches. The locations are marked
on the density plot in Figure ![]() . The plot is shaded
according to the accompanying key to indicate snowfall amounts for
March 13, 1993, for the eastern United States. Note: There are 640
acres in a square mile, one degree of latitude is approximately 69
miles, and one degree of longitude (in this region) is approximately
51 miles. Your numerical answers should be given in square mile-feet of snow.
. The plot is shaded
according to the accompanying key to indicate snowfall amounts for
March 13, 1993, for the eastern United States. Note: There are 640
acres in a square mile, one degree of latitude is approximately 69
miles, and one degree of longitude (in this region) is approximately
51 miles. Your numerical answers should be given in square mile-feet of snow.

![]() and the iterated integral
representation of a double integral over
and the iterated integral
representation of a double integral over ![]() , which is given by
Fubini's theorem (see Section 5.2 of the text). Let us first review
this connection.
, which is given by
Fubini's theorem (see Section 5.2 of the text). Let us first review
this connection.
![]() is defined by the inequalities
is defined by the inequalities
![]() and
and
![]() , where g1 and g2
are continuous functions of one variable. In order to partition
, where g1 and g2
are continuous functions of one variable. In order to partition
![]() into
into ![]() rectangular cells, we first partitioned
rectangular cells, we first partitioned ![]() into
M columns of width
into
M columns of width
![]() ,
,
![]() , and then
partitioned the ith column into N cells of height
, and then
partitioned the ith column into N cells of height
![]() . (See Figure
. (See Figure ![]() .) This led to a
Riemann sum for the total accumulation of f which could be written
as an iterated sum,
.) This led to a
Riemann sum for the total accumulation of f which could be written
as an iterated sum,
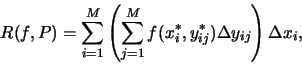
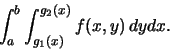
![\begin{figure}
\centering
\subfigure[]{\psfig{file=chapter5d/betweengraphs1.ps,h...
...=chapter5d/betweengraphs2.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img269.gif)
![]() is defined by
inequalities
is defined by
inequalities
![]() and
and
![]() ,
then we would first partition
,
then we would first partition ![]() into N rows, and then partition
each row into M cells. (See Figure
into N rows, and then partition
each row into M cells. (See Figure
![]() .) After writing out the corresponding
iterated sum form for the Riemann sum and evaluating the limit of
Riemann sums, we arrived at the following iterated integral,
.) After writing out the corresponding
iterated sum form for the Riemann sum and evaluating the limit of
Riemann sums, we arrived at the following iterated integral,
![]() lies between vertical lines x=a and x=b,
we first partitioned
lies between vertical lines x=a and x=b,
we first partitioned ![]() into columns and then partitioned the
columns, which ultimately gives an iterated integral first with
respect to y and then with respect to x; and when
into columns and then partitioned the
columns, which ultimately gives an iterated integral first with
respect to y and then with respect to x; and when ![]() lies
between horizontal lines y = c and y = d, we first partitioned
lies
between horizontal lines y = c and y = d, we first partitioned ![]() into rows and then partitioned the rows, which gives an iterated
integral first with respect to x and then with respect to y.
into rows and then partitioned the rows, which gives an iterated
integral first with respect to x and then with respect to y.
![]() and the iterated integral
representation of the integral of a function over
and the iterated integral
representation of the integral of a function over ![]() . As was the
case in the plane, this is given by Fubini's theorem. In particular,
we would like to introduce an intuitive way to think about this
connection in terms of sampling schemes. Let us work with a region
. As was the
case in the plane, this is given by Fubini's theorem. In particular,
we would like to introduce an intuitive way to think about this
connection in terms of sampling schemes. Let us work with a region
![]() defined by
defined by
![]() ,
,
![]() ,
and
,
and
![]() , where g1, g2, h1 and
h2 are continuous functions.
, where g1, g2, h1 and
h2 are continuous functions.
![]() , we will sample the value of f by inserting ``sensors'' on
``wires'' into
, we will sample the value of f by inserting ``sensors'' on
``wires'' into ![]() to record the values of f. For example, if
to record the values of f. For example, if
![]() represents a container of liquid and we want to find the total
heat of the liquid, we would insert
represents a container of liquid and we want to find the total
heat of the liquid, we would insert
![]() wires into the fluid
with N small temperature sensors on each wire to measure the
temperature in the container. Intuitively, we would insert the wires
parallel to the z-axis through the top of the container in a
rectangular pattern and the space the N sensors along the wires.
The pattern of the wires depends on the geometry of the projection
wires into the fluid
with N small temperature sensors on each wire to measure the
temperature in the container. Intuitively, we would insert the wires
parallel to the z-axis through the top of the container in a
rectangular pattern and the space the N sensors along the wires.
The pattern of the wires depends on the geometry of the projection
![]() of the region in the xy-plane. We would partition
of the region in the xy-plane. We would partition
![]() into
into ![]() cells as we did in Discussion 25, and
then insert one wire into each cell. In this case,
cells as we did in Discussion 25, and
then insert one wire into each cell. In this case,
![]() . (See Figure
. (See Figure ![]() .) Since
.) Since
![]() lies
between the graphs of functions of x, over an interval
lies
between the graphs of functions of x, over an interval
![]() , we would partition
, we would partition
![]() into L columns with Mcells in each column and then insert the
into L columns with Mcells in each column and then insert the
![]() wires into the
cells of the partition of
wires into the
cells of the partition of
![]() . The sensors should be placed
on the wires so that they are located above the graph of h1 and
below the graph of h2. This sampling scheme would
correspond to an iterated Riemann sum of the form
. The sensors should be placed
on the wires so that they are located above the graph of h1 and
below the graph of h2. This sampling scheme would
correspond to an iterated Riemann sum of the form
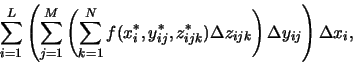
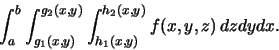
![\begin{figure}
\centering
\subfigure[]{\psfig{file=chapter5d/wires1.ps,height=2....
...fig{file=chapter5d/wires2.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img294.gif)
![]() had been described instead as lying between the graphs
of functions of y and z, we would have inserted the wires parallel
to the x-axis. The location of the wires would then be determined
by the description of the projection of
had been described instead as lying between the graphs
of functions of y and z, we would have inserted the wires parallel
to the x-axis. The location of the wires would then be determined
by the description of the projection of ![]() in the yz-plane.
Similarly, if
in the yz-plane.
Similarly, if ![]() had been described as lying between the graphs of
functions of y and z, we would have inserted the wires parallel to
the y-axis. The location of the wires would then be determined by
the description of the projection of
had been described as lying between the graphs of
functions of y and z, we would have inserted the wires parallel to
the y-axis. The location of the wires would then be determined by
the description of the projection of ![]() in the xz-plane.
in the xz-plane.
![]() and writing
out a corresponding iterated integral.
and writing
out a corresponding iterated integral.