The First Iteration

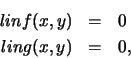
The method that we want to develop begins by replacing the functions f and g by their linear approximations. The point of this is that it is easy to solve systems of linear equations. Of course, the functions must be differentiable in order to write out a linear approximation. In addition, we must choose a base point for the linear approximation. Usually we think of this as a first guess to the solution we are seeking. The following two equations define the linear approximations.

    linf:=(x,y)-> f(x0,y0) +D[1](f)(x0,y0)*(x-x0)+D[2](f)(x0,y0)*(y-y0):
    ling:=(x,y)-> g(x0,y0) +D[1](g)(x0,y0)*(x-x0)+D[2](g)(x0,y0)*(y-y0):

Notice that we used the D operator to compute the derivative. For example, the partial derivative of with respect to the first variable, that is, x , is written D[1](f) . To evaluate it at the point (x,y), we use D[1](f)(x,y) . Let us choose a base point near our first root, say the point (1,1).

    x0:=1:y0:=1:

To see the values of the coefficient for the base point, we enter the following:

    linf(x,y);
    ling(x,y);

To generate our first approximation to the exact solution we must solve the system of linear equations:

$$\begin{eqnarray*}linf(x,y) &=& 0\\ ling(x,y) &=& 0, \end{eqnarray*}$$

which is, in this case,

$$\begin{eqnarray*}-3 + 2x + 2y &=& 0\\ 2 + x - 4y &=& 0. \end{eqnarray*}$$

The solution to these equations is (x,y) = (4/5,7/10). We can do this by hand or use the Maple command solve , which solves equations symbolically.

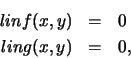
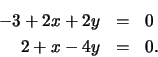
As with the original set of equations, we can interpret these equations graphically. Here we are finding the points of intersection of the level sets of linf and ling for the value 0. Since these functions are linear, their level sets are straight lines and this amounts to finding the point of intersection of two straight lines in the plane. The following will plot the level sets for f and for gfor the value 0 and the level sets for linf and ling for the value 0.

    A:=implicitplot({f(x,y)=0,g(x,y)=0},x=0..2,y=0..2,
                     scaling=CONSTRAINED,color=red):
    B:=implicitplot({linf(x,y)=0,ling(x,y)=0},x=0..2,y=0..2,
                     scaling=CONSTRAINED,color=blue):
    C:=plot([[x0,y0]],x=0..2,y=0..2,style=point,color=black):
    display([A,B,C]);

Notice that the point of intersection of the straight lines, (4/5,7/10), is closer to a true point of intersection of the curves than the initial guess, (1,1), but it is no better than our initial graphical approximation (.8,.6). However, we can repeat this approximation process by letting (4/5,7/10) be a new basepoint.