


Next: Parametric Curves and Vector
Up: Multivariable Calculus: Collaborative Learning
Previous: Discussion 18: Local Linearity
Euclidean Space and Vectors
startsection section10mm-.5 Discussion 1 Functions of Several Variables
In one variable calculus you considered functions of one independent
variable, which were written symbolically in the form
y = f(x).
Here we will be focusing for the most part on functions of two
independent variables, which can be written symbolically in the form
z= f(x,y).
Many of you have worked with functions of this form already, either at
the end of a one-variable calculus course, or in physics, chemistry or
biology. While the sciences may not use the standard mathematical
symbolism, they provide a wealth of examples of functions. In this
abbreviated discussion, we will explore what you know about functions.
One member of your group should be the scribe for the day. The
scribes job is to write a summary of your responses to each of the
following questions that should be handed in at the end of class.
startsection subsection10mm.5 Exercises
- 1.
- You have all explored function of one variable in precalculus and calculus. What are some of the questions you asked about these functions?
Discuss the different ways functions were represented as well as the mathematical techniques used to analyze these functions.
- 2.
- What, if any, contact have you had with functions of more than
one variable in a science? Provide examples of the functions where
possible. It is sufficient to describe the relevant quantities
in prose rather than symbols.
- 3.
- How
might the questions you asked about functions of one variable in calculus be relevant to functions of more than one variable? Are there other questions you
might ask about functions of more than one variable?
- 4.
- In order to help establish working groups, we need to know
more about our learning styles and our mathematical strengths and
weaknesses. Different students learn mathematics in different ways.
Some students are more visual -- they can understand more from
pictures and graphical displays of information. Others are more
computational -- they learn better through applications and problem
solving. Some students learn through patterns, that is, they see
several examples and work through several more on their own until they
can recognize general patterns. Others are able to understand general
structures and rules and then are able to use computational techniques
to fill in the details.
What are the mathematical strengths of each member of the group? What about the other strengths of group members, for example, who takes notes well; which members are willing to suggest ideas; who will ask questions when they don't understand? What strengths do you hope members of your group would contribute to the discussion?
startsection section10mm-.5 Discussion 2 The Coordinate System in 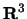
In this discussion, we will use the Euclidean coordinate system in
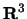 to describe subsets of
to describe subsets of 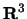 .
The sets will be
presented either in symbols or in prose, and you will have to
translate the description from one form into the other form and sketch
the set. Several of the prose descriptions are presented in the form
of a model from outside of mathematics.
.
The sets will be
presented either in symbols or in prose, and you will have to
translate the description from one form into the other form and sketch
the set. Several of the prose descriptions are presented in the form
of a model from outside of mathematics.
startsection subsection10mm.5 Exercises
- 1.
- For each of the following prose descriptions of subsets of
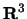 ,
sketch the subset and give a symbolic description of the subset in set
notation. For the last two parts of the problem, the context for the
description of the set is provided after the description of the set. It will
be helpful to understand the context before you answer the question.
,
sketch the subset and give a symbolic description of the subset in set
notation. For the last two parts of the problem, the context for the
description of the set is provided after the description of the set. It will
be helpful to understand the context before you answer the question.
- (a)
- The set of all points ``which are less than one unit from the origin.''
- (b)
- The set of all points ``inside a cube with sides of length two
centered at the point (1,1,1).''
- (c)
- The set of all points ``which are less than two units from the point (1,2,-1).''
- 2.
- For each of the following symbolic descriptions of subsets of
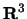 ,
sketch
the subset and give a prose description of the subset.
,
sketch
the subset and give a prose description of the subset.
- (a)
-
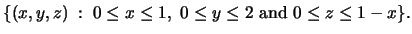
- (b)
-
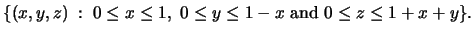
- (c)
-
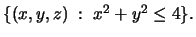
Figure:
The robot for exercise 3.
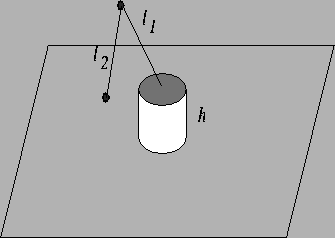 |
- 3.
- In programming the motion of a computer controlled robotic arm,
it is useful to have a mathematical description of the region of space
that can be reached by the grasping end of the arm given the location
of the base of the arm and the range of motion at each pivot. Here is
a particular example to think about. (See Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .)
.)
The base of the arm is located on a pedestal of height h and both
the lower portion and the upper portion of the arm have length 2h.
The arm can rotate in a complete circle on its pedestal and the only
constraint on the motion of the arm is that the angle between the
lower portion of the arm and the upper portion of the arm must be less
than or equal to 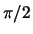 .
In your calculations, assume that the
pedestal is centered on the vertical axis and the base of the arm is
located at (0,0,h).
.
In your calculations, assume that the
pedestal is centered on the vertical axis and the base of the arm is
located at (0,0,h).
- (a)
- What is the radius of the largest circle in the (x,y)-plane that can
be reached by the grasping end of the arm?
- (b)
- The arm is designed to remove items from a conveyer belt on the
(x,y)-planethat is located a distance of h units from the vertical
axis. What is the length of the segment of the conveyer belt that is
accessible to the grasping end of the arm?
startsection section10mm-.5 Discussion 3 Using the Language of Vectors
In this discussion, we will use the language of vectors to describe
subsets of the plane and of space. In order to do this, we will use the correspondence we have established between vectors in the plane
or in space and points in 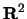 or
or 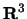 .
Each vector
.
Each vector 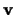 is placed with initial point at the origin, the point which corresponds to this vector is the endpoint of
is placed with initial point at the origin, the point which corresponds to this vector is the endpoint of 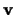 .
Thus the vector
.
Thus the vector
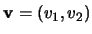 corresponds to the point
corresponds to the point
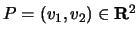 and the vector
and the vector
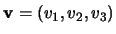 corresponds to the point
corresponds to the point
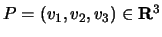 .
.
startsection subsection10mm.5 Exercises
In each of these exercises, use the correspondence above to describe
in words the subset of  or
or  which corresponds to
each set of vectors.
which corresponds to
each set of vectors.
- 1.
- Describe in words and sketch the set of points in the plane or in space
which corresponds to each set of vectors. In each case,
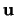 and
and
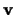 are fixed vectors.
are fixed vectors.
- (a)
- i.
-
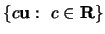
- ii.
-
![$\{ c{\bf u}: \ c \in [0,1] \} $](img24.gif)
- iii.
-
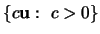
- iv.
-
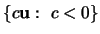
- (b)
- i.
-
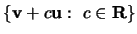
- ii.
-
![$\{ {\bf v}+ c{\bf u}: \ c \in [0,1] \}$](img28.gif)
- iii.
-
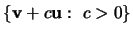
- iv.
-
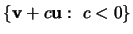
- 2.
- Describe in words and sketch the set of points in
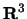 that
corresponds to each set of vectors. In each case,
that
corresponds to each set of vectors. In each case, 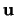 ,
,
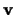 ,
and
,
and
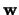 are fixed vectors.
are fixed vectors.
- (a)
- i.
-
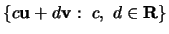
- ii.
-
![$\{ c{\bf u}+ d{\bf v}: \ c, \ d \in [0,1] \} $](img33.gif)
- iii.
-
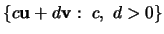
- (b)
- i.
-
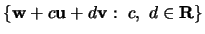
- ii.
-
![$\{ {\bf w}+ c{\bf u}+ d{\bf v}: \ c, \ d \in [0,1] \} $](img36.gif)
- iii.
-
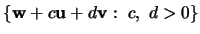
startsection section10mm-.5 Discussion 4 The Geometry of Lines and Planes
In this discussion, we want to use our descriptions of lines and planes to explore the possible geometric relationships between a line and a plane or between two lines in 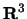 .
.
startsection subsection10mm.5 Exercises
- 1.
- (a)
- Suppose
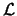 is a line in
is a line in 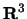 and
and 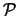 is a
plane in
is a
plane in 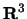 ,
what are the possible geometric relationships between
,
what are the possible geometric relationships between
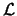 and
and 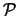 ?
?
- (b)
- Explain how you would determine what the geometric relationship is between a given line and plane.
- (c)
- Determine the relationship between each of the following lines and planes
- i.
- Suppose
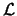 is the line
is the line
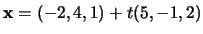 and
and 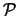 is the plane
x + 3y - z = 5.
is the plane
x + 3y - z = 5.
- ii.
- Suppose
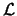 is the line
is the line
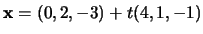 and
and 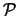 is the plane
x - y + 2z = 2.
is the plane
x - y + 2z = 2.
- 2.
- Suppose
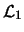 and
and
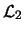 are distinct lines in
are distinct lines in 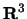 .
.
- (a)
- What are the possible geometric relationships between these lines? How would you determine the geometric relationship?
- (b)
- When would the two lines lie in a plane? How would you determine the plane which contains both lines?
- (c)
- What is the relationship between each of the following pairs of lines?
- i.
- The line through (1,2,1) with direction vector (1,1,-1) and the line through (-1,0,3) with direction vector (-1,2,1).
- ii.
- The line
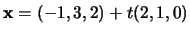 and the line
and the line
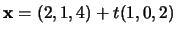 .
.
- iii.
- The line
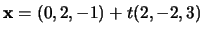 and the line
and the line
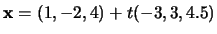 .
.
- 3.
- (a)
- Given three points in
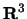 ,
how would you determine if the
points are collinear?
,
how would you determine if the
points are collinear?
- (b)
- Given four points in
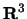 ,
how would you determine if the
points are coplanar, that is, if there is a plane containing all four
points?
,
how would you determine if the
points are coplanar, that is, if there is a plane containing all four
points?
- (c)
- For each of the following sets of points, determine if they are
collinear or coplanar. If so, find the line or plane which contains them.
- i.
-
P = (2,1,0),
Q = (1,3,-1),
R = (2,4,-3).
- ii.
-
P = (1,2,-3),
Q = (2,0,-1),
R = (-1,6,-7).
- iii.
-
P = (2,1,0),
Q = (1,3,-1),
R = (2,4,-3),
S = (1,-1,3).
- iv.
-
P = (1,2,-3),
Q = (2,0,-1),
R = (-1,6,-7),
S = (0,2,2).
startsection section10mm-.5 Discussion 5 Introduction to Optics
Optics is the study of the behavior of light, the visible and near
visible parts of the electromagnetic spectrum, as it moves through an
optical system. The optical system might be a single mirror or prism,
a zoom lens on a camera, a laser, or the human eye. Our goal in this
discussion will be to apply the language of vectors to develop several
fundamental concepts in optics. In the next discussion, we will use
the computer to create and analyze models of more complicated optical
systems that use the ideas we develop here.
In a uniform or homogeneous medium, like a gas or a lens, very narrow
beams of light travel in straight lines. In order to visual this, we
will think of ``light rays'' passing through a medium. When light
strikes a mirror or passes between media of different densities, the
rays change direction according to simple geometric rules. We will
represent a ray of light by a vector, a displacement vector,
indicating the path of light in a medium. The initial point of the
vector will be located at the source of the light or where the light
ray enters the medium and the endpoint will be located where the light
ray leaves the medium or at a ``viewing'' point. (See Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .)
.)
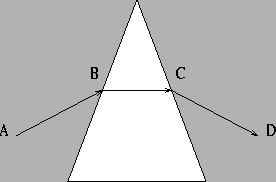
Figure:
A schematic diagram of light passing through a prism from
point A to point D. The vector
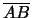 represents the light
in air, the vector
represents the light
in air, the vector
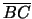 represents the light ray in the
prism, and the vector
represents the light ray in the
prism, and the vector
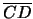 represents the light ray in air.
represents the light ray in air.
 |
The speed of light in a homogeneous medium is a constant which depends
on the density of the medium, the denser the medium, the lesser the
speed of light. The geometric rules for the behavior of light depend
on the relative speeds of light in adjacent media rather than the
actual speeds. Thus it will turn out to be useful to work with ratio
of the speed of light in a vacuum, c, to the speed of light v in a
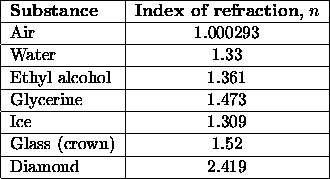
medium. The quotient, c/v is called the Index of refraction
of the substance, which we denote by n. The indices of refraction
of several common substances are shown in Figure ![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .
.
Figure:
Indices of refraction for some common substances.
 |
Fermat's Principle
The geometric rules that govern reflection and refraction can be
determined experimentally, but they are also a mathematical
consequence of the physical law known known as Fermat's
principle, after the mathematician Pierre de Fermat, who formulated
the principle in 1657. It states that light traveling between
two points follows the path which takes the least amount of time. We
can apply this principle to calculate the path that light takes when
reflected in a mirror and when it passes from one medium to another.
In order to carry out our calculations, it will be helpful to recall
the relationship between velocity, distance and time. If light
travels from P to Q in a homogeneous medium it follows the
straight line segment between the points. If L denotes the distance
between them, which is the length of the vector
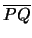 ,
and v is
the speed of light in the medium, it will take L/v units of time.
,
and v is
the speed of light in the medium, it will take L/v units of time.
Figure:
(a) A schematic diagram of a light ray reflecting off a plane mirror. (b) A schematic diagram of a light ray passing from a rarer medium to a denser medium.
![\begin{figure}\centering
\subfigure[]{\psfig{file=chapter1d/planemirror.ps,heigh...
...hapter1d/simplerefraction.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img54.gif) |
startsection subsection10mm.5 Exercises
- 1.
- Fermat's Principle for Reflection. In order to apply
Fermat's principle to a ray of light that travels from a point P to
a point R after being reflected off of a mirror at a point Q, we
must find the location Q that minimizes the total time for the path.
It will be sufficient to work in the plane. Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) contains a schematic diagram of a light ray
reflecting off a mirror. Rather than find the value of x which
minimizes time, we will find the angle I1 and I2 which
minimize time. Note that the angles are measured counterclockwise
from the line normal to the mirror at Q. The angle I1 is
called the angle of incidence and I2 is called the angle of reflection.
contains a schematic diagram of a light ray
reflecting off a mirror. Rather than find the value of x which
minimizes time, we will find the angle I1 and I2 which
minimize time. Note that the angles are measured counterclockwise
from the line normal to the mirror at Q. The angle I1 is
called the angle of incidence and I2 is called the angle of reflection.
- (a)
- Express the total time it takes to travel along the vectors
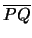 and
and
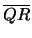 as a function of x. (Notice
that a, b, and d are constants.)
as a function of x. (Notice
that a, b, and d are constants.)
- (b)
- Find the sines of the angles I1 and I2 as functions of
x.
- (c)
- In order to minimize the total time as a function of x, we
must differentiate total time with respect to x and set the result
equal to 0. Use this differentiated expression to express
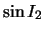 in terms of
in terms of
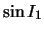 .
.
- (d)
- What does this tell you about I1 and I2?
- 2.
- Fermat's Principle for Refraction Now let us apply
Fermat's principle to a light ray that passes from a homogeneous
medium with index of refraction n1 to a homogeneous medium with
index of refraction n2, so that the speed of light in the first
medium is
v1 = c/n1 and the speed of light in the second
medium is
v2 = c/n2. Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) contains a schematic diagram for a light ray traveling from a point
P in the first medium to the interface of the two media at Q and
then on to the point R in the second medium. Once again we will
find the relationship between the I1, the angle of incidence and
I2, the angle of refraction, rather than the location of
Q.
contains a schematic diagram for a light ray traveling from a point
P in the first medium to the interface of the two media at Q and
then on to the point R in the second medium. Once again we will
find the relationship between the I1, the angle of incidence and
I2, the angle of refraction, rather than the location of
Q.
- (a)
- Express the total time it takes to travel along the vectors
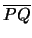 and
and
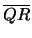 as a function of x. (Notice
that a, b, and d are constants.)
as a function of x. (Notice
that a, b, and d are constants.)
- (b)
- Find the sines of the angles I1 and I2 as functions of
x.
- (c)
- In order to minimize the total time as a function of x, we
must differentiate total time with respect to x and set the result
equal to 0. Use this differentiated expression to express
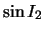 in terms of
in terms of
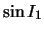 .
.
- (d)
- What does this tell you about I1 and I2?
Figure:
(a) Figure for Exercise 3. The image of an object located at P is
viewed from R. (b) Figure for Exercise 4. The refracted image of
an obect at P is viewed from R.
![\begin{figure}\centering
\subfigure[]{\psfig{file=chapter1d/reflection.ps,height...
...file=chapter1d/refraction.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img58.gif) |
- 3.
- When we perceive the image of an object in a mirror, we know
from experience that the image has been reflected and that the object
is located on our side of the mirror. Of course, on occasion we
can be fooled by a reflected image and we perceive it to be elsewhere
than it is. For example, suppose that you are located at the point
R in Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) and that you see the reflected
image of an object located at P. Thus your eye receives the ray of
light traveling from P to Q to R.
and that you see the reflected
image of an object located at P. Thus your eye receives the ray of
light traveling from P to Q to R.
- (a)
- If you were to be ``fooled'' by the image, where would you
perceive the object to be located?
- (b)
- Of course, images that we see in a mirror are reversed.
Why is this the case? Use a diagram to explain your answer.
- 4.
- Just as our eye can be fooled by a reflected image, it can be
fooled by a refracted image. For example, suppose that you are
located at R in
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) in the air and are looking
at an object at P in water. Thus your eye receives the ray
of light traveling from P to Q to R.
in the air and are looking
at an object at P in water. Thus your eye receives the ray
of light traveling from P to Q to R.
- (a)
- If you were to be ``fooled'' by the image, where would you
perceive the object to be located?
- (b)
- The size of objects that we see underwater are distorted. How
are they distorted and why? Use a diagram to explain your answer.
- 5.
- The relationship that you found between the angle of incidence
and angle of refraction in Exercise 2 can be used to give precise
answers to questions like those in Exercise 4. Say, for example, that
you are looking over the side of a boat on a calm lake at objects
under the surface of the water. Use the value 1.00 for the index of
refraction of air and 1.33 for the index of refraction of water.
(Remember that our observing an object means that a light ray travels
from the object to our eye.)
- (a)
- (See Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .) Suppose your eye is located two
feet above the surface of the water and you look at an object that is
three feet in diameter and four feet under the surface of the water.
How large does the object appear to you from your vantage point?
.) Suppose your eye is located two
feet above the surface of the water and you look at an object that is
three feet in diameter and four feet under the surface of the water.
How large does the object appear to you from your vantage point?
- (b)
- (See Figure
![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) .) Suppose that a small object is
located two feet under the surface of the water a lateral distance of
four feet from your location. Determine the angle between your line
of sight and the vertical segment
.) Suppose that a small object is
located two feet under the surface of the water a lateral distance of
four feet from your location. Determine the angle between your line
of sight and the vertical segment
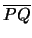 when you look at the
object. How deep under the water does the object appear to be?
when you look at the
object. How deep under the water does the object appear to be?
- (c)
- (Part (b) continued.) Suppose you move your head closer to the
water (along
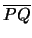 )
and the object remains located at R.
What happens to the angle between your line of sight and
)
and the object remains located at R.
What happens to the angle between your line of sight and
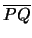 when you look at the object? In particular, what
happens when your eye approaches the surface of the water? Explain
your answer.
when you look at the object? In particular, what
happens when your eye approaches the surface of the water? Explain
your answer.
Figure:
(a) Figure for Exercise 5(a). (b) Figure for Exercise 5(b),(c).
![\begin{figure}
\centering
\subfigure[]{\psfig{file=chapter1d/lake1.ps,height=2.5...
...sfig{file=chapter1d/lake2.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img59.gif) |



Next: Parametric Curves and Vector
Up: Multivariable Calculus: Collaborative Learning
Previous: Discussion 18: Local Linearity
2000-08-31
![]()
![]() to describe subsets of
to describe subsets of ![]() .
The sets will be
presented either in symbols or in prose, and you will have to
translate the description from one form into the other form and sketch
the set. Several of the prose descriptions are presented in the form
of a model from outside of mathematics.
.
The sets will be
presented either in symbols or in prose, and you will have to
translate the description from one form into the other form and sketch
the set. Several of the prose descriptions are presented in the form
of a model from outside of mathematics.
![]() .
In your calculations, assume that the
pedestal is centered on the vertical axis and the base of the arm is
located at (0,0,h).
.
In your calculations, assume that the
pedestal is centered on the vertical axis and the base of the arm is
located at (0,0,h).
![]() or
or ![]() .
Each vector
.
Each vector ![]() is placed with initial point at the origin, the point which corresponds to this vector is the endpoint of
is placed with initial point at the origin, the point which corresponds to this vector is the endpoint of ![]() .
Thus the vector
.
Thus the vector
![]() corresponds to the point
corresponds to the point
![]() and the vector
and the vector
![]() corresponds to the point
corresponds to the point
![]() .
.
![]() or
or ![]() which corresponds to
each set of vectors.
which corresponds to
each set of vectors.
![]() .
.
![]() .)
.)

![]() .
.
![]() ,
and v is
the speed of light in the medium, it will take L/v units of time.
,
and v is
the speed of light in the medium, it will take L/v units of time.
![\begin{figure}\centering
\subfigure[]{\psfig{file=chapter1d/planemirror.ps,heigh...
...hapter1d/simplerefraction.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img54.gif)
![\begin{figure}\centering
\subfigure[]{\psfig{file=chapter1d/reflection.ps,height...
...file=chapter1d/refraction.ps,height=2.5in,width=2.5in,angle=270} }%
\end{figure}](img58.gif)