


Next: Differentiability in One Variable
Up: Differentiation of Real-Valued Functions
Previous: plot3d
The command ``contourplot3d'' is a version of the plot3d command which
shows horizontal slices of the graph of f. It displays 15 slices by
default. As with the contourplot command, slices can be set to a
different value with the ``contours='' option. The toolbar and
menubar for this command are identical to those for the plot3d
command. Here is an example of its use:
contourplot3d(f(x,y),x=-2..2,y=-2..2);
(For more information, click on contourplot3d .)
startsection subsection10mm.5 Exercises
The following exercises ask you to analyze the plots described above
for three functions of increasing complexity. You should insert your
answers directly into this worksheet. Your answers should include the
particular plotting commands that you use, the resulting plots, and
prose responses as indicated. Your answers should be edited, that is,
your descriptions should be written in complete sentences and you
should include only the relevant plot commands and graphics. When you
are done, delete the material that precedes the exercises from the
document and save the worksheet under a new name. (To save this
worksheet, click on ``save as'' in the pull-down ``File'' menu in the
menu bar of this window. Be sure to save the worksheet as a file of
type .mws . )
If you have not already done so, execute the following command to load
the
with(plots):
- 1.
- Let
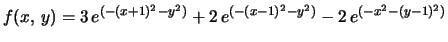 ,
which can be defined by:
,
which can be defined by:
f:=(x,y) -> 3*exp(-(x+1)^2 - y^2) +2*exp(-(x-1)^2 - y^2)
- 2*exp(-x^2 - (y-1)^2);
- (a)
- Use the command ``plot3d'' to plot the graph of f on the
rectangle
![$[-3,3]\times[-3,3]$](img178.gif) .
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
.
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
- (b)
- Use the ``contourplot'' command to plot the contours of f on the
same domain. (You may want to adjust the number of contours.)
Describe the contours of f on this domain. In particular, what is
the behavior of the contours at the extreme points of f? Further,
what is the behavior of the contours near the point (.2,-.4)? Why
should we single out this point for special attention?
- 2.
- Let
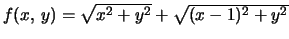 .
We can define this function in Maple by entering the input
line:
.
We can define this function in Maple by entering the input
line:
f:=(x,y) -> sqrt(x^2 + y^2) + sqrt((x-1)^2 +y^2);
- (a)
- Use the command ``plot3d'' to plot the graph of f on the
rectangle
![$[-3,3]\times[-3,3]$](img178.gif) .
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
.
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
- (b)
- Use the ``contourplot'' command to plot the contours of f on the
same domain. (You may want to adjust the number of contours.)
Describe the contours of f on this domain. In particular, what is
the behavior of the contours at the extreme points of f?
- (c)
- Are there qualitative differences between the extreme points of
this function and those of the function in part a? Explain your
answer. Refer to plots as necessary.
- 3.
- Let
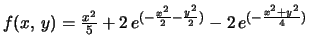 .
We can define this
function in Maple by entering the input line:
.
We can define this
function in Maple by entering the input line:
f(x,y) := (x,y) -> x^2/5 + 2*exp(-x^2/2 - y^2/2 )
-2*exp(-(x^2 +y^2)/4);
Analyze the behavior of f using any or all of the commands we
have used so far and any of their options. Note there are at least
five points of interest that must be explained. It may be necessary
to use different plot ranges and types of plots to identify them.
startsection section10mm-.5 Discussion 16 Rates of Change
In Section 3.1, we developed an intuitive understanding of the rate of change of functions
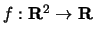 and
and
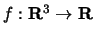 by
analyzing contour plots and the graph of the function. We have not
yet developed a symbolic technique which would allow us to determine
an exact numerical value for the rate of change of a function of
several variables. In this discussion we will use a contour plot to
begin to develop the idea of the instantaneous rate of change of a
function
by
analyzing contour plots and the graph of the function. We have not
yet developed a symbolic technique which would allow us to determine
an exact numerical value for the rate of change of a function of
several variables. In this discussion we will use a contour plot to
begin to develop the idea of the instantaneous rate of change of a
function
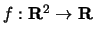 .
.
startsection subsection10mm.5 Exercises
- 1.
- We will begin with a review of rates of change for functions of one
variable. Let
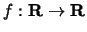 be a function and p a
fixed point in the domain of f.
be a function and p a
fixed point in the domain of f.
- (a)
- What is the average rate of change of f over the interval
[p,q], where q is another point in the domain of f? Express your
answer in prose and in symbols.
- (b)
- How do we obtain the instantaneous rate of change of f at p
from the average rate of change of f over an interval? Express your
answer in prose and in symbols.
- (c)
- What information about f do you need in order to carry out the
calculation of the instantaneous rate of change of f? If this
information is not available, what information would you need to
approximate the instantaneous rate of change? How would you do the
approximation? What information would you need in order to improve on
this approximation and how would you use it?
- 2.
- Now let us consider a particular function f of two variables, the
altitude function for the region in New Hampshire including Stinson
Mountain. We are interested in computing the average and
instantaneous rate of change of the altitude function along a path. We
will work from a contour map of the region. (Note that the altitude
change between adjacent contour lines on the plot is 40 feet and the
scale of the map is indicated in the legend.)
- (a)
- Suppose that P and Q are fixed points on the contour map. Let
us consider the line segment from P to Q. How would you compute
the average rate of change of the altitude function over this segment?
Express your answer in prose and in symbols.
- (b)
- How would you compute the instantaneous rate of change of the
altitude function along this segment at P? Express your answer in
prose and symbols.
- (c)
- What information would you need to carry out the calculation of the
instantaneous rate of change in 2(b)? Is it possible to obtain this
information from a contour map? Explain. If it is not possible to obtain
this information from a contour map, explain how you would approximate
the instantaneous rate of change from the contour map.
- (d)
- Let us focus on the trail on the map leading up the side of Stinson
Mountain. Let P be the point where the trail crosses the 1600
ft. contour and let Q be the point where the trail crosses the 1800
ft. contour. The trail is reasonably straight between these two
points. Apply your method from 2(a) to calculate the average rate of
change of the altitude function on this path from P to Q.
- (e)
- If possible, use the method you described in 2(b) to calculate the
instantaneous rate of change of the altitude function along this path at the
point P. If it is not possible, calculate the approximation to the rate of
change that you described in 2(c).
- 3.
- We will continue to use the particular point P described in
Exercise 2(d). Choose a point Q0 on the contour plot, different
from the original Q and consider the line segment from P to Q0.
As above, it is possible to compute the instantaneous rate of change
of the altitude function along the segment from P to Q0. In
general, this instantaneous rate of change will not be the same as the
value you computed in Exercise 2(e), thus we should think about how
the instantaneous rate of change of the altitude function at P along
a line segment depends upon the point Q0 chosen.
- (a)
- Suppose Q0 lies on the line from P through the original point
Q. What is the relationship between the instantaneous rate of change of altitude at
P along the line segment from P to Q0 and the instantaneous
rate of change of altitude at P along the line segment from P to Q ?
Explain your answer.
- (b)
- Now suppose Q0 is any point on the contour plot different from P. For which points Q0 will the instantaneous rate of change of altitude at
P along the line segment to Q0 be positive? Indicate these
points on the contour plot and justify your choice.
- (c)
- For which points Q0 will the instantaneous rate of change of altitude at
P along the line segment to Q0 be negative? Indicate these
points on the contour plot and justify your choice.
- (d)
- For which points Q0 will the instantaneous rate of change of altitude at
P along the line segment to Q0 be zero? Indicate these points
on the contour plot and justify your choice.
Figure:
A contour plot of the region near Stinson Mt. in New Hampshire.
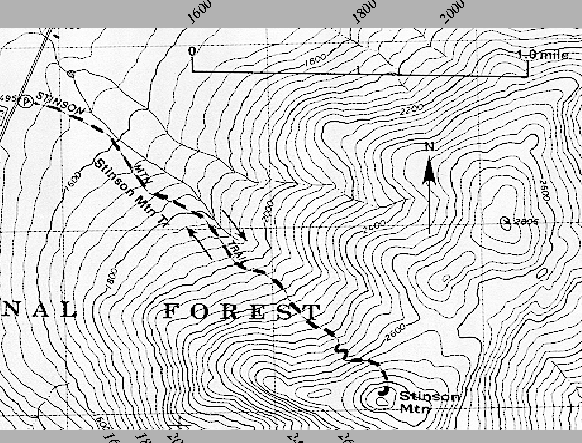 |
startsection section10mm-.5 Discussion 17 Local Linearity of Functions of Two Variables
This is a LATEXversion of a Maple worksheet. The worksheet is available in the directory
/home/stu/courses/math141.
startsection subsection10mm.5 Introduction
In this Maple worksheet we will explore the differentiability of
functions of two variables. In particular we would like to investigate the relationship between the existence of the partial derivatives of f at a point and the differentiability of f.



Next: Differentiability in One Variable
Up: Differentiation of Real-Valued Functions
Previous: plot3d
2000-08-31
![$[-3,3]\times[-3,3]$](img178.gif) .
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
.
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
![$[-3,3]\times[-3,3]$](img178.gif) .
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
.
Locate the extrema (maxima and minima) of
f and describe the behavior of f on the domain.
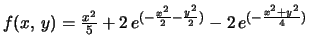 .
We can define this
function in Maple by entering the input line:
.
We can define this
function in Maple by entering the input line:
