Integration on Curves

startsection section10mm-.5 Discussion 32 Riemann Sums on Paths in Space

 

In our previous discussions, we have used Riemann sums to approximate the total value of a physical quantity over a region in the plane or in space. Now we will turn our attention to the problem of approximating the total value of a function defined on a path in the plane or in space.

We will begin with an example from physics. Let us consider the charge on an insulated copper wire in the presence of a stationary electric field. Since the wire is insulated the electric charge, that is, the free electrons, in the wire cannot leave the wire. However, since copper is a conductor, the charge will move freely in the wire in response to the electric field until it reaches an equilibrium distribution. This distribution can be represented by a charge density function $\rho$ that is defined on the wire. Generally, the charge will be unevenly distributed in the wire, so that $\rho$ will not be constant. The total charge of the wire is the total accumulation of the charge density function over the length of the wire.

We would like to approximate the total charge of the wire. As you might expect, the approximation will take the form of a Riemann sum, thus we will partition the wire, sample the charge density in each cell of the partition, scale these sampled values and sum the scaled values over the cells or the partition. In this case, the Riemann sum will use a parametrization of the curve in space which represents the wire.

The goal of this discussion is to carry our this process, that is, to construct a Riemann sum to approximate the total charge in the wire.

startsection subsection10mm.5 Exercises

Suppose we have a charged wire in space. Let us assume that we can measure the charge density of the wire at any point and that $\rho$ is measured in coulombs per centimeter. Finally, let us assume that the wire is represented by the image of a parametrization $\boldsymbol{\alpha}\: : \: [a,b] \subset {\bf R}\rightarrow {\bf R}^3$, that is, by the set $\{ \boldsymbol{\alpha}(t) = (x(t),y(t), z(t)) \: : \: a \leq t \leq b \}$

1.

(a)

Sketch a picture of a charged wire in space.

(b)

How would you use the parametrization to partition the wire into N cells? Give a complete description of this partition, including a description of a typical cell in the partition.

(c)

How would you choose a sampling point in the i^th cell of the partition?

(d)

Add the partition and sampling points to your sketch for N=8. Label the cells of the partition and the sampling points.

2.

(a)

What is the scaling factor for the i^th cell? Can you compute this exactly?

(b)

How would you use the parametrization to compute the scaling factor? (Exactly if possible, otherwise approximately.)

3.

(a)

Use the partition, sampled charge density values and scaling factors to construct a Riemann sum to approximate the total charge of the wire.

(b)

How would you increase the number of cells in the partition in order to improve this approximation?

4.

Based on our previous work with Riemann sums, we expect that to calculate an exact value for the total charge of the wire, we should take the limit of the Riemann sum approximations as the dimensions of the cells approach zero. Can you evaluate the limit in this case? Explain why or why not.

startsection section10mm-.5 Discussion 33 Path Independence

 

We have seen that the line integral of a vector field over a curve does not depend on the parametrization of the curve, but it does depend on the direction of motion along the curve. In this discussion, we will begin to investigate how the line integral of a vector field in ${\bf R}^2$ depends on the path. Initially, we will compute a number of examples of line integrals. We will then compile these results and try to determine if there are any noticeable patterns in the results. The goal will be to use these examples to make a conjecture about the dependence of a line integral on the path.

In each question below, there is a set of three parametrizations of different paths and a set of three vector fields. In each set of parametrizations, the functions $\boldsymbol{\alpha}$ and $\boldsymbol{\beta}$ parametrize different paths between the same two points and the function $\boldsymbol{\gamma}$ parametrizes a closed path. In each set of vector fields, the third vector field is a gradient vector field.

startsection subsection10mm.5 Exercises

For each of the following questions, first describe and sketch the paths parametrized by the functions $\boldsymbol{\alpha}$, $\boldsymbol{\beta}$, and $\boldsymbol{\gamma}$, then compute the line integrals $\int_{\boldsymbol{\alpha}} {\bf F}\; ds$, $\int_{\boldsymbol{\beta}} {\bf F}\; ds$, and $\int_{\boldsymbol{\gamma}} {\bf F}\; ds$ for each vector field ${\bf F}$. Your writeup for each question should consist of your descriptions, sketches, and the values of the line integrals computed. The values should be entered on the chart that follows the exercises.

1.

The parametrizations are

(a)

$\boldsymbol{\alpha}(t) = (t, t^2)$ for $0 \leq t \leq 1$.

(b)

$\boldsymbol{\beta}(t) = (t^2, t)$ for $0 \leq t \leq 1$.

(c)

$\boldsymbol{\gamma}(t) = (\sin t, \cos t)$ for $0 \leq t \leq 2\pi$.

The vector fields are ${\bf F}(x,y) = (x,y)$, ${\bf F}(x,y) = (x,xy)$ and ${\bf F}(x,y) = \nabla f(x,y)$ for f(x,y) = xy.

2.

The parametrizations are

(a)

$\boldsymbol{\alpha}(t) = (\sin t, \cos t)$ for $0 \leq t \leq \pi/2$.

(b)

$\boldsymbol{\beta}(t) = (t, 1-t^2)$ for $0 \leq t \leq 1$.

(c)

$\boldsymbol{\gamma}(t) = \left\{ \begin{array}{ll} (t,t^2)&\mbox{ for }0 \leq t \leq 1 \\ (2t-t^2,2-t)&\mbox{ for } 1 \leq t \leq 2. \end{array}\right.$

The vector fields are ${\bf F}(x,y) = (x,y)$, ${\bf F}(x,y) = (x,xy)$ and ${\bf F}(x,y) = \nabla f(x,y)$ for f(x,y) = xy.

3.

The parametrizations are

(a)

$\boldsymbol{\alpha}(t) = (t \cos (2 \pi t), t \sin(2 \pi t))$ for $0 \leq t \leq 1$.

(b)

$\boldsymbol{\beta}(t) = (t, \sin(\pi t))$ for $0 \leq t \leq 1$.

(c)

$\boldsymbol{\gamma}(t) = \left\{ \begin{array}{ll} (t,t^3)&\mbox{ for }0 \leq t \leq 1 \\ (2t-t^2,2-t)&\mbox{ for } 1 \leq t \leq 2. \end{array}\right.$

The vector fields are ${\bf F}(x,y) = (x,y)$, ${\bf F}(x,y)= (y,x)$ and ${\bf F}(x,y) = \nabla f(x,y)$ for f(x,y) = x²+2y.

4.

The parametrizations are

(a)

$\boldsymbol{\alpha}(t) = (1+ \cos t, \sin t)$ for $0 \leq t \leq \pi/2$.

(b)

$\boldsymbol{\beta}(t) = (2-t,t)$ for $0 \leq t \leq 1$.

(c)

$\boldsymbol{\gamma}(t) = \left\{ \begin{array}{ll} (2t,0)&\mbox{ for }0 \leq t... ...\ (1-\cos(\pi t), \sin(\pi t))&\mbox{ for } 1 \leq t \leq 2. \end{array}\right.$

The vector fields are ${\bf F}(x,y) = (x,y)$, ${\bf F}(x,y)= (y,x)$ and ${\bf F}(x,y) = \nabla f(x,y)$ for f(x,y) = x²+2y.

5.

The parametrizations are

(a)

$\boldsymbol{\alpha}(t) = (t, \cos ( \pi t))$ for $0 \leq t \leq 1$.

(b)

$\boldsymbol{\beta}(t) = (t, 1-2t^2)$ for $0 \leq t \leq 1$.

(c)

$\boldsymbol{\gamma}(t) = \left\{ \begin{array}{ll} (t \sin(\pi t), t \cos(\pi ... ... }0 \leq t \leq 1 \\ (0, t-2)&\mbox{ for } 1 \leq t \leq 2. \end{array}\right.$

The vector fields are ${\bf F}(x,y) = (x,y)$, ${\bf F}(x,y) = (x^2, xy)$ and ${\bf F}(x,y) = \nabla f(x,y)$ for f(x,y) = x²y.

6.

The parametrizations are

(a)

$\boldsymbol{\alpha}(t) = (1 + \sin t,1 + \cos t)$ for $0 \leq t \leq \pi/2$.

(b)

$\boldsymbol{\beta}(t) = (t + 1, 2-t^2)$ for $0 \leq t \leq 1$.

(c)

$\boldsymbol{\gamma}(t) = \left\{ \begin{array}{ll} (2t,(2t-1)^2)&\mbox{ for }0 \leq t \leq 1 \\ (4-2t,1)&\mbox{ for } 1 \leq t \leq 2. \end{array}\right.$

The vector fields are ${\bf F}(x,y) = (x,y)$, ${\bf F}(x,y) = (x^2, xy)$ and ${\bf F}(x,y) = \nabla f(x,y)$ for f(x,y) = x²y.

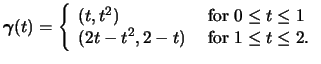
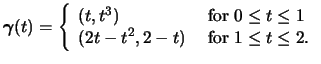
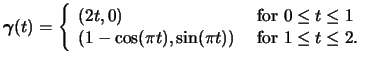
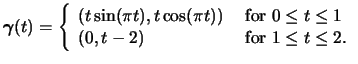
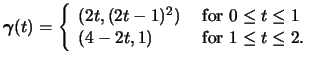
startsection section10mm-.5 Discussion 34 Green's Theorem

 

In Section 6.3 of the text we introduced Green's Theorem for regions in the plane which are bounded by a piecewise differentiable simple closed curve. The precise statement of Green's Theorem is as follows.

Let ${\cal R}$ be a region in the plane whose boundary ${\cal C}$ is a piecewise differentiable simple closed curve that is positively oriented with respect to ${\cal R}$. Let ${\bf F}(x,y) = (u(x,y),v(x,y))$ be a vector field which is defined and continuously differentiable on a neighborhood containing ${\cal C}$ and ${\cal R}$. Then

Recall that the positive orientation of the boundary of ${\cal R}$orients the curve so that the interior of ${\cal R}$ remains on the left as you traverse the curve.

In this discussion we will explore an extension of Green's Theorem to regions with more complicated boundaries.

startsection subsection10mm.5 Exercises

1.

In class we have given a statement of Green's Theorem for a region ${\cal R}$ in the plane which is bounded by a single piecewise differentiable simple closed curve ${\cal C}$. Here we will develop a statement of Green's theorem which applies to more general regions. Let ${\cal R}$ be the region

$$\{ (x,y) \: : \: 1 \leq x^2 +y^2 \leq 4\ \}$$

Let ${\bf F}(x,y) = (u(x,y),v(x,y))$ be a continuously differentiable vector field defined on a neighborhood containing ${\cal R}$.

(a)

Sketch the region ${\cal R}$ and describe its boundary

(b)

In order to apply Green's Theorem, we will partition this region into two regions each of which is bounded by a simple closed curve. Let ${\cal R}_1$ be the portion of ${\cal R}$ lying above the x-axis and let ${\cal R}_2$ be the portion of ${\cal R}$ lying below the x-axis. The boundary of each of these regions is a simple closed curve which is made up of four differentiable curves. Sketch these regions and describe each boundary.

(c)

Orient each boundary so that you can apply Green's Theorem to ${\cal R}_1$ and ${\cal R}_2$. Use Green's Theorem to express $\int \int_{{\cal R}_1} (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}) \: dA$ as the sum of the line integral of ${\bf F}$along the pieces of the boundary of ${\cal R}_1$. Do the same for ${\cal R}_2$.

(d)

Since ${\cal R} = {\cal R}_1 \cup {\cal R}_2$, we know that

$$\int \int_{\cal R} (\frac{\partial v}{\partial x} - \frac{\pa... ...partial v}{\partial x} - \frac{\partial u}{\partial y}) \: dA.$$

Use this result and your answer to part c. to express the double integral over ${\cal R}$ as a line integral of ${\bf F}$ along the curves making up the boundary of ${\cal R}$.

2.

Let ${\cal R}$ be a region whose boundary consists of the union of a finite number of piecewise differentiable, simple closed curves. Such a region can be obtained from the interior of a cimple closed curve ${\cal C}_1$ by removing the interiors of a collection of simple closed curves ${\cal C}_2$,..., ${\cal C}_n$.

(a)

Sketch an example of such a region.

(b)

Based upon your answer to Exercise 1, give a careful statement of Green's Theorem for regions of this type. Be sure to explain how you would orient each piece of the boundary of ${\cal R}$.