The Foundations of Analysis: Basic Definitions

Now we have a definition that utilizes a new idea, the greatest lower bound, or infimum, which has yet to be defined, and some basic ideas from analysis and set theory that we have not reviewed. Further, there really is something to prove now in order to show that our measure has all the desired properties. So we must address three groups of questions, only the last of which is directly about measure: questions about infimums, sequences and series; questions about the number of elements in a set, which is not the same as the measure of a set, and whether or not this proposed definition satisfies the desired properties. In this discussion set we will focus on the first set of questions, keeping in mind that we ultimately want to be able to prove that our definition of measure is a good one.

Before we can ask the questions, we must define the objects of study.

We are all familiar with the basic algebraic properties of real numbers concerning the operations of addition and multiplication, commutativity, associativity, distributivity, existence of inverses, etc. For those who have had algebra, these properties are the axioms for a field. There are further algebraic properties of R having to do with the ordering of the real numbers. For example, if c > 0 and a < b, then ac < ab. There is a further property that we will take as given, the completeness axiom. This is usually stated in terms of upper bounds, but it could be stated in terms of lower bounds just as easily.

First, recall that if $S \subset {\bf R}$, a number b is an upper bound for S, if for every $x \in S$, $x \leq b$. Then b is called the least upper bound or supremum of S if (i) b is an upper bound for S and (ii) no number less than b is an upper bound for S. We denote the supremum of S by $\sup S$. Similarly we can define lower bound and greatest lower bound or infimum. Then we have

Completeness Axiom for R
Every nonempty set S of real numbers which is bounded above has a supremum; that is, there exists real number b with $b = \sup S$.

While it may appear that the sup of a set and limits are the same, they are not. The existence of a sup for a set bounded above is a property of R that we take as an axiom for the real numbers. A limit is a value whose existence must be verified for a particular type of set. Strictly speaking, a sequence of real numbers is a function $a:{\bf N} \rightarrow {\bf R}$. We usually suppress the function notation and write a_n rather than a(n) and speak of a_n as being an element or term of the sequence. Also, we will express a sequence by writing $\{a_{1},a_{2}, \ldots\}$, $\{a_{n}\}_{n = 1, \ldots \infty}$, or simply $\{a_{n}\}$.

$L \in {\bf R}$ is the limit of the sequence a_n if for every $\epsilon > 0$ there exists an N so that

$$\mid a_{n} - L \mid < \epsilon$$

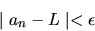
for all n > N. We write $\lim_{n \rightarrow \infty} a_{n} = L$.

Infinite series are a particular type of sequence that is obtained by a summation construction. Given a sequence a_n, we can construct a new sequence s_n by letting $s_{n} = a_{1} + a_{2} + \ldots + a_{n}$. This sequence is usually written in summation notation

$$\sum_{i = 1}^{\infty} a_{i}$$

We say that s_n is the sequence of partial sums of the series $\sum_{i = 1}^{\infty} a_{i}$. When we refer to the sum of the series, we mean the limit of the sequence of partial sums,

$$\lim_{n \rightarrow \infty} s_{n}$$

Now that we have our basic definitions, we may proceed.