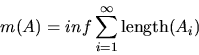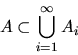In fact, we noted that the set
![]() falls outside of this
collection (although we argued that as the complement in [0,1] of a
countable set, it should have measure 1.) Since it is uncountable
and it contains no intervals of positive length, there is no way to
build up this set or its measure from that of intervals. This example
shows that we cannot extend the notion of length to all sets simply by
using the properties and that we are forced to define measure more
generally.
falls outside of this
collection (although we argued that as the complement in [0,1] of a
countable set, it should have measure 1.) Since it is uncountable
and it contains no intervals of positive length, there is no way to
build up this set or its measure from that of intervals. This example
shows that we cannot extend the notion of length to all sets simply by
using the properties and that we are forced to define measure more
generally.
Naively, we want to use the containment property above in combination
with countable additivity to ``shrink wrap'' sets. Let us suppose A is
a bounded set. Then A is contained in an interval
![]() ,
so
,
so
![]() .
At first, we may want to say that the measure of
A should be the length of the smallest interval containing A, but
that is inadequate since A might come in several pieces. This leads
us to say that the measure of A should be the sum of the lengths of
the ``smallest'' intervals that can be used to cover A.
Unfortunately, smallest is not precise enough here, and, in fact, there
is no way to specify a smallest collection. Rather for each such
``cover'', we want to look at the sum of the measures of the covering
subsets. Then, we want to look at the greatest lower bound, or
infimum of these values.
.
At first, we may want to say that the measure of
A should be the length of the smallest interval containing A, but
that is inadequate since A might come in several pieces. This leads
us to say that the measure of A should be the sum of the lengths of
the ``smallest'' intervals that can be used to cover A.
Unfortunately, smallest is not precise enough here, and, in fact, there
is no way to specify a smallest collection. Rather for each such
``cover'', we want to look at the sum of the measures of the covering
subsets. Then, we want to look at the greatest lower bound, or
infimum of these values.