


Next: About this document ...
Up: Seminar in Analysis Discussion
Previous: The Foundations of Analysis:
Some of these questions are basic questions we must get straight in
order to work with sequences and sets, but others are motivated
directly by our interest in measure. So far we have worked intuitively
and descriptively, describing in symbols those properties of a measure
that follow from our geometric intuition about length. In order to
develop these concepts with any assurance that they are mathematically
valid, we must provide a rigorous foundation for further work.
While every statement for supremums has a corresponding statement for
infimums, for the purposes of measure, we are interested in infimums,
thus the preference for infimums in some of the following questions.
- 1.
- What is the relationship between supremums (and infimums) and
limits?
- (a)
- Is a sup always a limit? If so, prove it, if not, provide a
counterexample.
- (b)
- Is a limit always a sup? If so, prove it, if not, provide a
counterexample.
- 2.
- (a)
- Given the above definitions of measure in terms of infimums and
the properties that we want a measure to satisfy, what do we want to
know about infimums? Your answer should be in the form of properties
for infimums.
- (b)
- Explain why you chose each of these properties based on your
understanding of measure.
- (c)
- Prove each of your properties.
- (d)
- What other properties of infinums, if any, might be useful in
the future? Prove one of them.
- 3.
- Since the definition of measure also uses infinite series, hence,
sequences, answer the previous question for sequences and series.
- 4.
- Using the above definition of measure
- (a)
- Prove that if
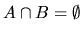 then
then
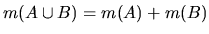 .
.
- (b)
- Prove directly (not appealing to the union property) that if
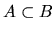 ,
,
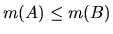 .
.
- (c)
- Prove that the measure is countably additive.



Next: About this document ...
Up: Seminar in Analysis Discussion
Previous: The Foundations of Analysis:
2000-03-07
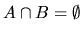 then
then
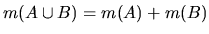 .
.
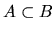 ,
,
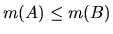 .
.