


Next: A definition of measure
Up: Seminar in Analysis Discussion
Previous: Introduction
In the first discussion we began to think about the concept of measure,
with the goal being to construct a set function
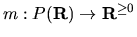 that extends the notion of length to sets
that are not intervals. Following the discussion questions the groups
agreed upon the following properties that we would want a measure to
satisfy:
that extends the notion of length to sets
that are not intervals. Following the discussion questions the groups
agreed upon the following properties that we would want a measure to
satisfy:
- 1.
- The measure of the empty set is 0:
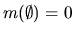 .
.
- 2.
- The measure of an interval is its length:
where I is an open, closed or half open interval with endpoints a < b.
That is, I = (a,b), [a,b), (a,b], or [a,b].
- 3.
- If
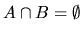 ,
then
,
then
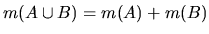 .
.
There were other properties involving set containment, intersection and
difference that followed from the union property. For example,
the union property implies that if
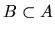 ,
then
m(A) = m(A - B)
+ m(B). Since m is always non-negative, it follows that
,
then
m(A) = m(A - B)
+ m(B). Since m is always non-negative, it follows that
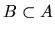 implies that
implies that
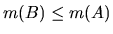 .
.
We also saw that the union property can be extended to arbitrary
finite unions of mutually disjoint sets:
This property is called finite additivity of a measure. Its
proof required the use of mathematical induction. But, we
also realized that we wanted to extend this further, to infinite
disjoint unions because of our example of a countable set
![${\bf Q} \cap
[0,1]$](img9.gif) that we want to have measure zero. So we will add the
following, more general version of additivity, called countable
additivity, to our list of properties:
that we want to have measure zero. So we will add the
following, more general version of additivity, called countable
additivity, to our list of properties:
if
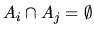 for all
for all 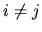 .
.
A neglected property
There is one further property, called translation invariance, that
seems self-evident, but will turn out to have rather subtle
consequences. First, we need a definition: Given a subset
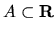 and
and
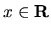 ,
we define
,
we define
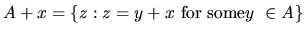 .
Notice that A is a set and x is an
element, but A + x is defined to be a set. Then, we will say that
the measure is translation invariant if for any
.
Notice that A is a set and x is an
element, but A + x is defined to be a set. Then, we will say that
the measure is translation invariant if for any
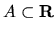 and
and
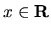 ,
m(A + x) = m(A).
,
m(A + x) = m(A).



Next: A definition of measure
Up: Seminar in Analysis Discussion
Previous: Introduction
2000-03-07
![]() ,
then
m(A) = m(A - B)
+ m(B). Since m is always non-negative, it follows that
,
then
m(A) = m(A - B)
+ m(B). Since m is always non-negative, it follows that
![]() implies that
implies that
![]() .
.
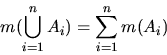
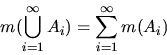
![]() and
and
![]() ,
we define
,
we define
![]() .
Notice that A is a set and x is an
element, but A + x is defined to be a set. Then, we will say that
the measure is translation invariant if for any
.
Notice that A is a set and x is an
element, but A + x is defined to be a set. Then, we will say that
the measure is translation invariant if for any
![]() and
and
![]() ,
m(A + x) = m(A).
,
m(A + x) = m(A).