CSCI 262 Data Structures--Spring 2004

Assignment 4 Solutions

Problem 1: Polynomial Calculator programs:

queue.cc

polynomial.cc

polyCalc.cc

Problem 2: Solution to Ackermann function:

a) ackermann.cc

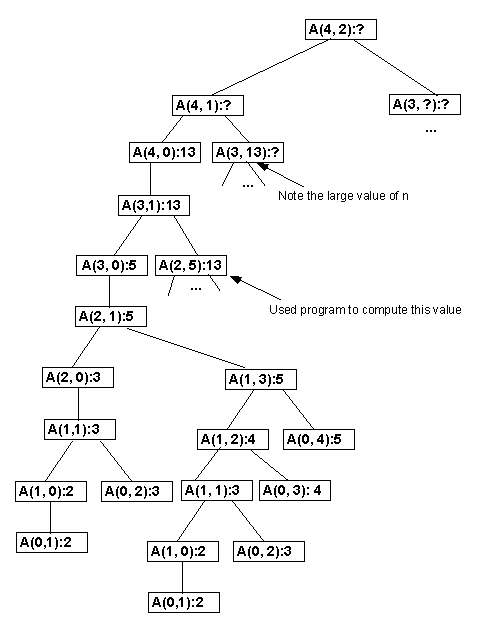
b) What happens when you try to compute Ackermann(4, 2)?
When you try to compute Ackermann(4, 2), the computation does not finish (at least not for a long time). This is so because, as shown in the tree below, the value of n increases as the recursive calls are made. For a recursive function to finish, each call must bring us closer to a base case. However, here we have made a call that seems to take us farther from the base case, since n becomes 13 (after starting out at 2). One would expect this to take a long time to compute (if it actually ever finishes!).

To interpret the following recursion tree, take note that the general case of the Ackermann function calls itself twice:

return ackermann(m-1, ackermann(m, n-1));

In order to execute this, the call to ackermann(m, n-1) must be performed first so that its return value can be used in the outer call to ackermann. These two calls are represented as two branches of the recursion tree. The following is only a portion of the recursion tree for a call to ackermann(4, 2). Note that to compute ackermann(4, 1), we must first compute ackermann(3, 13). n is getting much larger and not getting closer to the base case. In fact, if you try to run ackermann(3, 13) it also takes a very long time (if it ever finishes!).