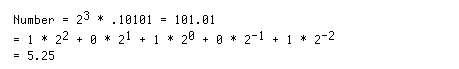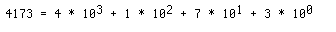
CSCI 150, Spring 2003

Binary representations.

1. Types of information
We use computers to represent many different types of information:

• Numbers
• Symbols (letters, punctuation, etc.)
• Pictures
• Sound
• Program instructions

Computers do all their computations using digital circuits, which can only represent things with 1's and 0's.

By combining 1's and 0's in different patterns and sequences, can represent complex pieces of information and compute solutions to difficult problems.

2. Counting in Base 2 (binary)
Base 10 uses 10 digits - 0 through 9.
Base 2 uses only 2 digits - 0 and 1

Decimal (Base 10)	Binary (Base 2)
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010

In base 10, each place represents a power of 10:

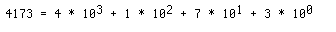
In base 2, each place represents a power of 2:

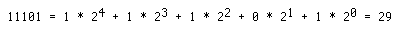
3. Converting from Decimal into Binary:
Divide repeatedly by 2. Put remainders in reverse order:

	25/2 = 12 	Remainder 1
	12/2 = 6  	Remainder 0
	6/2 = 3 	Remainder 0
	3/2 = 1 	Remainder 1
	1/2 = 0 	Remainder 1

Therefore, 25 is 11001 in base 2

4. Hexadecimal is Base 16

   Base 10    Base 16
     0          0
     1          1
     2          2
     3          3
    ...       ...

     9          9
    10          A
    11          B
    12          C
    13          D
    14          E
    15          F
    16         10
    17         11
    ...        ...
   255         FF
   256        100

Converting Binary to Hexadecimal:
Each group of 4 binary digits (bits) is 1 hexadecimal digit.

1011 0011 = B 3

5. Binary arithmetic
a) Representing positive and negative numbers:
Signed Magnitude:

First digit is sign bit: 0 for positive and 1 for negative
Remaining digits represent value

+3 = 00000011
-3 = 10000011

First digit is sign bit as above.
If negative, take value and FLIP all bits

+3 = 00000011
-3 = 11111100

First digit is sign bit as above.
If negative, take one's complement and add 1.

+3 = 00000011
-3 = 11111101

Adding numbers:
Convert to two's complement and add:

    14 =    00001110
  + 11 =    00001011
  ___________________
    25      00011001

Subtracting numbers:
Convert to two's complement and add:

     14 =    00001110 =    00001110
   - 11 =  - 00001011 =	 + 11110101
   _________________________________
      3        ???         00000011

Potential problems:

    127 =     01111111
   + 60 =   + 00111100
   _____________________
    187       10111011 = -69     OVERFLOW!

6. Representing real numbers
32 bit representation:

• 1 bit for sign
• 7 bits for exponent
• 24 bits for fraction

0 1000011 101010000000000000000000

Sign = 0: Number is positive
Exponent = 3
Fraction = .10101