CSCI 150, Spring 2003

Recursion

1. Recursion is a special case of Divide and Conquer problem solving
One powerful technique for solving big problems is to divide the big problem into smaller problems, each of which is easier to solve. Recursion can be used to solve problems in which these smaller subproblems are smaller versions of the original problem.

2. Writing Recursive Procedures:
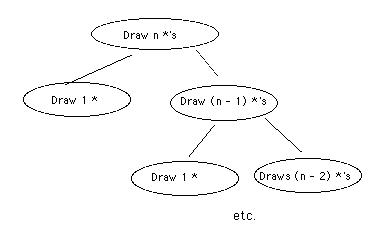
Example: Write a procedure to draw n stars, where n is an integer parameter.

Strategy:

1) Draw 1 star
2) Draw (n - 1) stars

Picture:

Pascal Code:

program drawing;
procedure drawStars( n : integer );
begin
	if n < = 0 then	{Stopping condition or base case}
	begin
		{do nothing}
	end
	else			{General case }
	begin
		write( '*' );
		drawStars( n - 1 );
	end;
end;
begin
	drawStars(3);
end.

3. Rules for Recursive procedures (or functions).

• A recursive procedure or function is a procedure or function that calls itself.
• The subtasks must be smaller than the original problem.
• There must be a base case that specifies the stopping condition to avoid an infinite recursion.

4. Classic examples of Recursion: Factorial

n! = 1* 2 * 3 * ... * (n-1) * n (pronounced łn factorial˛)

n! = n * (n-1)!

Factorial(n) = n * Factorial (n - 1 ) for n > 0
Factorial(0) = 1

Pascal Code:

function factorial( n: integer): integer;
begin
	if n <= 0 then
	begin
		factorial := 1;		{return the value of 1}
	end
	else
	begin
		factorial := n * factorial( n-1 );	{return n*(n-1)! }
	end;
end;

5. Classic examples of Recursion: Fibonacci

Fibonacci sequence: 1 1 2 3 5 8 13 ...

Fib(n) = Fib(n-1) + Fib(n-2) for n > 1
Fib(0) = 0
Fib(1) = 1

Pascal Code:

function fib( n: integer): integer;
begin
	if n <= 1 then
	begin
		fib := n;		{return the value of 0 or 1}
	end
	else
	begin
		fib := fib(n-1) + fib(n-2);	
	end;
end;