Laboratory 9 Solutions

CSCI 132 Data Structures--Spring 2014

Laboratory 9 Solutions

Solutions to programs:

Comparison of sorting methods:

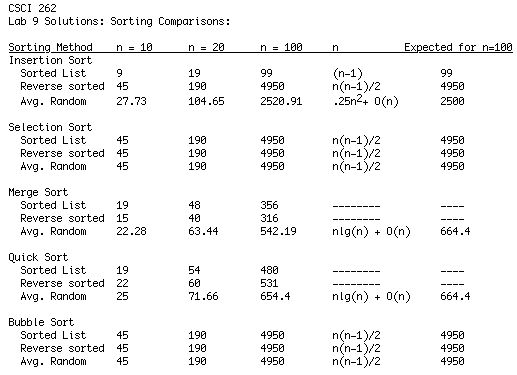
Problem 1d.
How to the sorting algorithms compare for each of the types of lists tested (sorted in order, sorted in reverse order, random)?

Answer:Selection sort and insertion sort are the same for a reverse sorted list, but insertion sort does better for a sorted list and on average for random lists.

Quick sort and Merge sort perform comparably, and both do considerably better than insertion sort and selection sort for the reverse and average random cases. However, they do not do quite as well as insertion sort for a sorted list.

Problem 2b.
What is the formula for the number of comparisons performed by bubble sort in each of the conditions tested? How did you arrive at this formula?

Answer:The Bubble Sort formula comes from the fact that for each pass through the inner loop, there are i-1 comparisons for a sublist of length i. With each pass through the outer loop, the size of the sublist decreases by 1 each time (starting with n and ending with 2). Thus the total number of comparisons is:

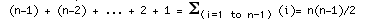
The running time for Bubble sort is independent of the list order.

Problem 2c.
How does the performance of bubble_sort() compare to the other sorting functions tested in this lab?

Answer:Bubble sort is the same as selection sort, which is generally worse than all the other algorithms.