CSCI 132 Data Structures--Spring 2014

Laboratory 8 Solutions

Solutions to programs:

searchCompare.cc

Problem 2:
a. Average number of comparisons for n = 5, 10, 20, 100, 1000

Successful:	n = 5	n = 10	n = 20	n = 100	n = 1000
Sequential	3.23	5.97	11.43	55.17	547.31
Binary 1	3.41	4.42	5.37	7.64	10.94
Binary 2	3.5	5.12	6.34	10.78	17.04
Unsuccessful:
Sequential	5	10	20	100	1000
Binary 1	3.36	4.38	5.36	7.68	10.98
Binary 2	5.36	7.12	9.14	13.7	19.96

b) Explain your results for a for a list length of 100 based on the formulas for the running time of each of the search algorithms given in the text.

The results match what would be expected from the formulas fairly well. They are a little different from the exact predicted values (as might be expected due to the randomized testing). The following are the expected and computed numbers for n = 100:

Successful	Computed	Expected	Formula
Sequential	55.17	50.5	(n+1)/2
Binary 1	7.64	7.64	lg(n) + 1
Binary 2	10.78	10.28	2lg(n) - 3
Unsuccessful	Computed	Expected	Formula
Sequential	100	100	n
Binary 1	7.68	7.64	lg(n) + 1
Binary 2	13.7	13.28	2lg(n)

c) For what values of n does sequential search do fewer average comparisons than binary_search_1?

Successful searches: Sequential search does fewer comparisons for n = 2, 3, 4, and 5.

Unsuccessful searches: Sequential search does fewer comparisons for no values of n.

d) For what values of n does sequential search do fewer average comparisons than binary_search_2?

Successful searches: Sequential search does fewer comparisons for n = 2, 3, 4, 5, and 6.

Unsuccessful searches: Sequential search does fewer comparisons for n = 1, 2, 3, 4, 5.

e) For what values of n does binary_search_2 do fewer average comparisons than binary_search_1?

Successful searches: Binary 2 does fewer comparisons for n = 3 and 4.

Unsuccessful searches: Binary 2 does fewer comparisons for no values of n.

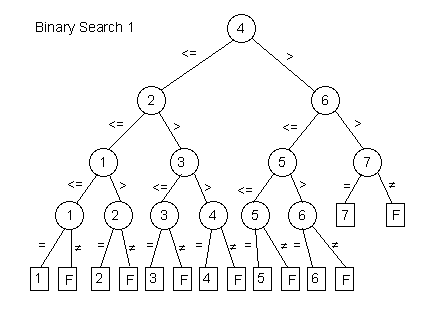
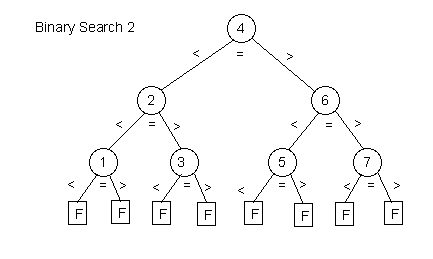
f) Draw the comparison trees for binary_search_1 and binary_search_2 for n = 7.

Home | | Syllabus | | Assignments | | Lecture Notes