
Home | | Syllabus | | Assignments | | Lecture Notes
1. Sorting methods (Implementation and analysis of running time for each): Insertion Sort (For contiguous and linked lists) Selection Sort Merge sort for linked lists Recursion tree for merge sort Quick sort for contiguous lists Partitioning lists Best and worst case analysis Comparison trees for sorting methods Lower bound for comparison based sorting Comparison of sorting methods 2. Tables Tables of different shapes Rectangular, Triangular, Jagged and Inverted Tables Row major order Column major order Index function Access arrays Tables as an Abstract Data Type Tables vs. Lists Radix Sort Hash Tables Computing a hash function (Truncation, folding, modular arithmetic) Resolving collisions Linear and Quadratic Probing Key dependent increments Random probing Chaining Implementation of a hash table Analysis of hash tables: Likelihood of collisions Counting number of probes made 3. Binary Trees Traversing trees (pre-order, in-order and post-order) Expression trees Linked implementation of binary trees Binary Search Trees Searching, inserting and removing nodes Tree sort 4. Graphs Undirected, Directed and Weighted graphs Representation with adjacency list Representation with adjacency matrix Breadth First Traversal Depth First Traversal
The following problems are intended to help you study for the exam, however topics not covered here may be on the exam as well. Use your text, class notes, labs and assignments to review for the exam as well.
1) Below are several functions for computing the square of a number. For each function, what is the Big-Oh estimate of the runtime for this code, and how did you arrive at it?
a) int square(int n)
{
return n*n;
}
b) int square(int n)
{
int answer = 0;
for (int i = 0; i < n; i++){
answer += i+i+1;
}
return answer;
}
c) int square(int n)
{
int answer = 0;
for (int i = 0; i < n; i++){
for (int j = 0; j < n; j++){
answer++;
}
}
return answer;
}
2) Explain what the best case and worst case situations are for QuickSort. What is the running time for each of these cases and how do you arrive at that running time?
3) A tri-diagonal matrix is a square matrix in which all entries are 0 except possibly those on the main diagonal and on the diagonals immediately above and below it. That is, T is a tri-diagonal matrix means that T(i, j)= 0 unless |i - j| <= 1 as shown below. Devise a space-efficient storage scheme for tri-diagonal matrices, and give the corresponding index function.

4) Trace the action of radix sort on the following list of 3 digit numbers:
5) Write a function to insert an entry into a hash table using linear probing. (Assume the hash function has been written and returns an integer location for an entry to be stored in the table).
}
6) The following list of numbers is an access array for a table. Draw the 2D table that is represented by this array. What is the index function that indicates the start of each table row?
| 0 | 1 | 4 | 9 | 16 | 25 |
7) Write a recursive function that will interchange all left and right subtrees of a binary tree. The function should take one parameter, a pointer to the root (or subroot) of the tree (or subtree) to be interchanged.
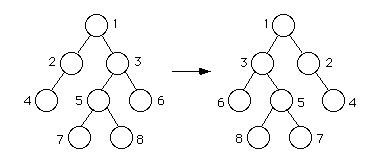
template <class Entry>
void Binary_tree<Entry>::recursive_interchange(Binary_node<Entry> *sub_root) {
}
8 a)Trace the steps that insertion sort will take to sort the following list of numbers from lowest to highest. For each step, indicate the number of comparisons made.
12 19 33 26 29 35 22
b) Write the formula for the average number of comparisons made by insertion sort for a random list. How close is the total number of comparisons above to the average number predicted by the formula?
9. Consider the following graph:
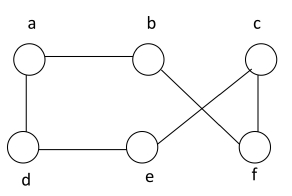
a) Draw a representation of this graph using adjacency lists.
b) If you start with vertex a, what order will the vertices be visited using breadth first traversal? If there is a choice between two vertices, visit them in alphabetical order.
c) If you start with vertex a, what order will the vertices be visited using depth first traversal? If there is a choice between vertices, visit them in alphabetical order.
Home | | Syllabus | | Assignments | | Lecture Notes