CSCI 132 Data Structures--Spring 2014

Review for Exam 2

Home | | Syllabus | | Assignments | | Lecture Notes

Topics:

1. Queues as Linked Lists
   Append(), Serve() and Retrieve() for linked list implementation
   Destructor, Copy Constructor and Assignment overload for Queue linked-list
   Representing polynomials as queues
   Polynomial calculations
2. Recursion
   Divide and Conquer using recursion
   Base Case (Stopping condition)
   General Case
   Classic recursive functions (Factorial, Fibonacci, Hanoi)
   Recursion trees
   Running time of recursive algorithms
   Tail Recursion
   Writing tail recursion as a while loop
   Writing trace of recursive functions
   Backtracking
   Look ahead
   Game trees
   Minimax method
3. Lists
   List operations (e.g. Insert, remove, retrieve, replace, etc).
   Class templates
   Contiguous implementation
   Linked-list implementation
   Doubly linked lists
4. Search
   Sequential search
   Binary search
   Differences between binary-search-1 and 2
   
   Analysis of running time of different search algorithms
   Comparison trees
   Tree terminology: height, vertex (node), root, leaf, level, parent, child
   External path length of trees
   Internal path length of trees
   Finding maximum and average number of comparisons from a comparison tree
5. Asymptotic analysis
   Relating one function to another using limits
   Ordering of constant, log, polynomial, exponential functions
   Big-O notation (and little-o, etc.)

Practice Problems

1) Write a function, Error_code interleave(List &list1, List &list2, List &list3) to interleave the entries of two lists (list1 and list2) together and put the resulting list into list3. Thus list3 has entries that alternate between the entries of list1 and list2. If one list has more entries than the other, the extra entries are omitted.
You should make use of the public functions defined in the list class.

class List {
 public:
    // methods of the List ADT
    List( );
    int size( ) const;
    bool full( ) const;
    bool empty( ) const;
    void clear( );
    void traverse(void (*visit)(List_entry &));
    Error_code retrieve(int position, List_entry &x) const;
    Error_code replace(int position, const List_entry &x);
    Error_code remove(int position, List_entry &x);
    Error_code insert(int position, const List_entry &x);
 protected:
    // data members for a contiguous list implementation
    int count;
    List_entry entry[max_list];
 };

2) For each of the following pairs of functions, use O notation to write how f(n) compares to g(n). I.e. write f(n) is o(g(n)), O(g(n)), Theta(g(n)), Big-Omega(g(n)), or little-omega(g(n)). Explain each of your answers.

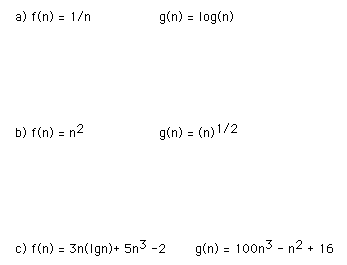
3) Draw the comparison tree for binary search 2 for a list of length 8. What is the height of the tree? What is the External path length of the tree? What is the Internal path length of the tree? What is the average number of comparisons made for successful searches? For unsuccessful searches?

4) Consider a function, f, defined as follows:

	f(n) = f(n-1) + f(n/2) for n > 2
	f((n) = n for n <= 2

a) Write the recursive function, int compute_f(int n), that computes f(n) for some integer n.

b) Draw the recursion tree for compute_f(6).

5) Consider the following recursive function:

	int foobar(int n, int ans) {
		if (n <= 0) {
			return ans;
		} else {
			return foobar(n-1, ans + n*n);
		}
	}

a) Fill in the following table for the values that n and ans take on in each recursive function call, starting with the function call, foobar(5, 0) (Note there may be more rows than you need).

n	ans	return value
5	0

b) Rewrite the foobar function using a while loop: int foobarWhile(int n)

6) Write the function, remove() for a doubly linked list.

template <class List_entry>
Error_code List<List_entry> :: remove(int position, List_entry &x)
/* Post: If 0 <= position < n, where n is the number of entries in the List, the function 
succeeds:
The entry in position is removed from the List, and the entries in all later positions 
have
their position numbers decreased by 1. The parameter x records a copy of the entry
formerly in position. Otherwise the function fails with a diagnostic error code. */
{
	Node<List_entry> *old_node, *neighbor;
	if (count == 0) return fail;
	if (position < 0 || position >= count) return range_error;

	//fill in the rest of the code here

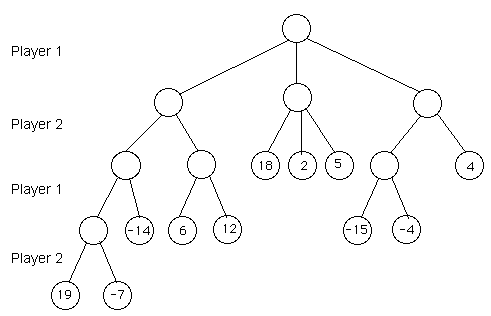
7) Consider the game tree for the (fictitious) game, fisbin, given below. Starting with the given values for each of the possible game endings use the minimax method to fill in the values of the other nodes in the tree. Assume that player 1 likes larger values and player 2 likes smaller values.

Home | | Syllabus | | Assignments | | Lecture Notes