CSCI 132 Data Structures

    Home | | Syllabus | | Assignments | | Lecture Notes

    Laboratory 5
    Due at the beginning of class, Wednesday, 3/12

    In today's lab you will practice writing recursive programs, writing tail recursions and converting a tail recursion to a while loop.

    1. Fibonacci numbers

    a) Write a program, fibRec.cc, that inputs a number n and outputs the fibonacci number for month n. Your main function should ask for and read in a positive integer from the user, and then call a recursive function,

      int fibRec(int n)

    that recursively computes the fibonacci number for n. The main function should print out the value returned by fibRec. Recall the following formula:

      fib(n) = n for n < 2;
      fib(n ) = fib(n-1) + fib(n-2)       for n >=2;

    Compile your program using the compile command:

      g++ -g -Wall fibRec.cc -o fibRec

    Sample output
    The following are some sample runs of the program: 

      radius% ./fibRec
Enter an integer: 5
The fibonacci number for month 5 is 5
radius% ./fibRec
Enter an integer: 6
The fibonacci number for month 6 is 8
radius% ./fibRec
Enter an integer: 7
The fibonacci number for month 7 is 13
radius% ./fibRec
Enter an integer: 38
The fibonacci number for month 38 is 39088169
radius% ./fibRec
Enter an integer: 39
The fibonacci number for month 39 is 63245986
radius% ./fibTail
Enter an integer: 40
The fibonacci number for month 40 is 102334155
    Also try running fibRec for n = 46. Time how long it takes to compute the solution. When you are done, print out the code for fibRec. Write on the printout the approximate number of seconds it took to run fibRec for n = 46.

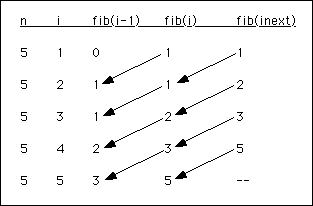
    b) In lecture we talked about a way to think about a tail-recursive version of the fibonacci program. We made a table of values that looks as follows for n = 5:

    Save your fibRec.cc file as fibTail.cc. Change your main function so that it calls a function, int fibIter(int n). fibIter() should call the function:

      int fibTail(int n, int i, int fib_i_minus1, int fib_i)

    The function fibTail() should update the values of i, fib_i_minus1 and fib_i as diagrammed above for each recursive call to itself (n is not updated, but it is passed as a parameter each time). When i == n, fibTail() should return fib_i. The initial values of n, i, fib_i_minus1 and fib_i set by fibIter should be n, 1, 0, 1, respectively (where n is the parameter passed to fibIter by the main function).

    Test your fibTail function with the same numbers as for part a. Print out your code and write on the code the approximate number of seconds needed to compute the fibonacci number for n= 46 using the tail recursion.

    c) Save the fibTail.cc file as fibWhile.cc. Re-write the Tail recursion as a while loop. You will no longer need the helper function, fibIter. Instead, your main function should call:

      int fibWhile(int n)

    which should compute the fibonacci number of n by updating the variables i, fib_i_minus1 and fib_i inside the body of the loop. Note that you will need to introduce a temporary variable, fib_i_next, to compute the next fibonacci number before updating fib_i_minus1 and fib_i. Test your code on the above numbers. Print out the source code and write on the paper the approximate number of seconds it took to compute the fibonacci number for n=46 using the while loop.

    2. Computing the coefficients for Pascal's triangle

    a) Write a program, pascal.cc that computes and prints out the coefficients of pascal's triangle for the first n rows. Start by writing a recursive function,

      int coeff(int n, int k)

    that computes C(n, k) recursively. It should make use of the following formula:

      C(n,0) = 1 and C(n, n) = 1 for n >= 0.
      C(n, k) = C(n-1, k) + C(n-1, k-1) for n > k > 0      .

    First, write your main function to test your coeff function with several different values of n and k (remember to keep k <= n).

    When you are convinced that coeff works correctly, modify your main function to input some positive integer from the user. It should then compute all the coefficients in Pascal's triangle (with n ranging from 0 to the number entered and k ranging from 0 to n).

    Sample Output
    Your output should look as follows: 

      radius% ./pascal
Enter an integer greater than zero: 7
1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1 
1 6 15 20 15 6 1 
radius%

    b) On a separate sheet of paper, draw the recursion function invocation tree for the call coeff(5, 3).

    What To Turn In.

    • A printout of the fibRec.cc file, with the number of seconds for fib(46) written on it.
    • A printout of the fibTail.cc file, with the number of seconds for fib(46) written on it.
    • A printout of the fibWhile.cc file, with the number of seconds for fib(46) written on it.
    • A printout of the pascal.cc file.
    • The function invocation tree for coeff(5, 3)
    • Submit your lab with the submit function:
        ~csci132/bin/submit csci132 lab5

    Be sure that the file prologue for each file contains your name, course, lecture section, date and purpose of the program or a description of the contents of the file.

    Reminder.
    Be sure to save a copy of each file in your labs directory. It is your responsibility to keep the copies of all programs written for this course until your graded assignment is returned.

    Home | | Syllabus | | Assignments | | Lecture Notes