CSCI 132 Data Structures
Assignment 5
Due at the beginning of class, Friday, March 21, 2014Home | | Syllabus | | Assignments | | Lecture Notes
Programming Style: You will be graded not only on whether your programs work correctly, but also on programming style, such as the use of informative names, good comments, easily readable formatting, and a good balance between compactness and clarity (e.g. do not define lots of unnecessary variables, or write multiple statements to perform a task that can be expressed clearly in a single statement.) Create appropriate functions for tasks that can be encapsulated.
Problem 1: Solving mazes
In class we learned about solving the eight queens problem using recursion with backtracking. The idea was that, starting from a particular configuration of queens, we would place a queen on a square, try to find a solution (recursively), then remove the queen from that square and try another square. In this problem you will use a similar strategy to solve acyclic mazes. From a given position on the maze, the function will move to an adjacent square, try to solve the maze, then move back to the original space. It will continue by moving to another adjacent square, until it finds a solution or until all adjacent squares have been tried without success. Like Theseus, who used a ball of string to keep track of his path as he moved through the labyrinth under King Minos' palace in Crete to slay the minotaur, this program will mark a path as it takes each successive move. When it backtracks, it will unmark the path (Think of Theseus winding up the ball of string as he backtracks out of the labyrinth).
First, copy the files for this assignment which can be found in:
-
~csci132/assignments/assign5
The files that you need for this problem are:
- maze.cc
maze.h
solveMaze.cc
The maze.h and maze.cc files have all the functions needed to create a maze and represent a path through the maze. You will only be writing functions in the file solveMaze.cc. You can compile this program with the command:
- g++ maze.cc solveMaze.cc -o solveMaze
This will prompt for the width and height of a maze, build the maze and print it out. This version does not solve the maze. If you run solveMaze, it will look something like the following:
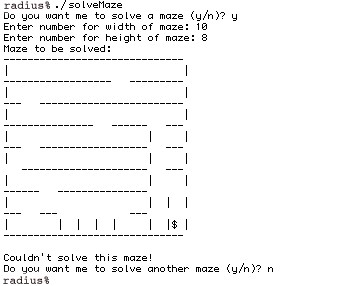
The maze is represented as an n x m grid (a 2-D array named maze_postion[n][m]). Each square in the grid can take on an integer value. The value of each square is initialized to zero except for the "end" of the maze, which is set to a value of 2. As the program moves through the maze, it should set the values of squares on the current path to 1 (this will allow the print-out to show the path when the program reaches the goal).
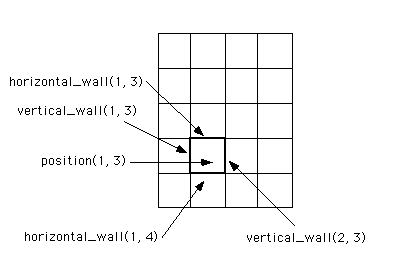
Walls of the maze are represented by two 2-D arrays: horizontal_wall[n][m+1], and vertical_wall[n+1][m]. The values of the elements of these arrays are false for those positions with no wall and true for positions where there is a wall. The positions of the walls relative to the grid are as follows:
- For a grid cell at position x, y,
- The horizontal wall directly above it is at horizontal_wall[x][y].
- The horizontal wall directly below it is at horizontal_wall[x][y+1].
- The vertical wall directly to the left is at vertical_wall[x][y].
- The vertical wall directly to the right is at vertical_wall[x+1][y].
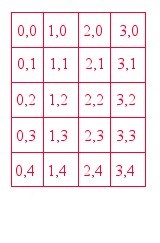
Note that an increase in y indicates a move downward in the maze. The relationship of the walls and the gridlines is diagrammed below; the grid on the right shows the corresponding x and y coordinates for each grid position:
You must write a program to find a path from the start (at positions 0,0) to the end (marked/displayed with a $). As you move through the maze, you are not allowed to move through a wall. Thus, before you make any moves you must test whether there is a wall in the way.
Your task is to write the function solveMaze(). This will recursively solve the maze and print out the solution if it finds one. It will return a value of true if it finds the end of the maze, and false if it does not find the end (a grid space with value of 2). For the moment the end of the maze is always at the corner, but your program should work no matter where the end of the maze is placed. In order to write this function you should write the following auxilliary functions: isWallAbove(), isWallBelow(), isWalltoLeft() and isWalltoRight( ). Thus you need to fill in the following functions:
- bool solve(Maze &theMaze, int x, int y)
Solve the maze from position x, y. If a solution is found, print it out and return a value of true. If no solution is found, return false. - bool isWallAbove(Maze &theMaze, int x, int y)
Return true if there is a wall above maze position x, y; return false otherwise. - bool isWallBelow(Maze &theMaze, int x, int y)
Return true if there is a wall below maze position x, y; return false otherwise. - bool isWalltoLeft(Maze &theMaze, int x, int y)
Return true if there is a wall to the left of the maze; return false otherwise. - bool isWalltoRight(Maze &theMaze, int x, int y)
Return true if there is a wall to the right of the maze; return false otherwise.
You will be able to make use of the following public maze functions:
- void print_maze( )
Print out the maze. If a cell has value 0, leave it blank. If a cell has value 1, print an X in the cell. If a cell has value 2, print a $ (to mark the end). - void set_position(int x, int y, int val)
Set the cell at position x, y to value given by val. - int get_position(int x, int y)
Returns the value of grid cell at position x, y. - int get_width()
Returns the width of the maze. - int get_height()
Returns the height of the maze. - bool is_horizontal_wall(int x, int y)
Return true if there is a horizontal wall at position x, y. Return false otherwise. - bool is_vertical_wall(int x, int y)
Return true if there is a vertical wall at position x, y. Return false otherwise.
Before you start working on this problem, you should write some short test functions to see what happens when you call these different maze functions. Familiarize yourself with the performance of these functions. You may also look at the implementation of these functions in the maze.cc file.
Start by implementing the auxilliary functions, (isWallAbove() etc.), since you will need these to implement solve(). The function, solve() should be a recursive function that uses backtracking to try out possible solutions. If no solution is found along a given path, the function will backtrack and try a different route. No path to a solution will ever cross itself for these acyclic mazes, so if the function ends up on a square that is already on the current path, it should return false and backtrack. Use the following strategy:
- If you are at the end of the maze (cell at position x, y is marked by value 2), print it out and return true.
- If you are on a marked cell (marked by value 1), you have already visited that square, so you should return false (you can't solve the maze by going in that direction).
- If you are on an unmarked cell, you should first mark the cell (set the value to 1).
For each of the cells adjacent to the current cell (up, down, left or right), if there is no wall between the current cell and the adjacent cell try to solve the maze from the adjacent cell. If you don't solve the maze, try another of the adjacent cells. After either solving the maze or unsuccessfully trying all 4 adjacent positions, unmark the cell you are on (set its value to zero). Return true if you solved the maze from one of the adjacent positions and false if you failed to solve the maze from any of the positions.
Important note: Your code for the function, solve(), should be short. My solution is under 30 lines. If you find yourself writing a very long function, you are on the wrong track.
Take a lot of time to think out this problem and make sure you understand the details before you attempt to write the solution.
Sample Output: