MATH 392 -- Coding Theory Seminar

Discussion 1 Solutions

February 4, 2002

A) Recall that this question dealt with three different scenarios for a communication

system and asked you to compare the efficiency and reliability of communication

over a binary symmetric channel with transmitting bits per

second:

1) words of length with no error-control coding

2) words of length , encoded with a parity check bit,

to codewords of length

3) words of length 11, encoded with 4 parity check bits

to words of length , giving a code with

Scenario 1.

words transmitted per second:

> wps1:=evalf(10^5/11);

The probability of at least one error in a received word is

> p:=.999;

> errorprob1:=1-p^11;

(decimal approximation). This means that on average, we will have:

> wps1*errorprob1;

or about 100 words per second containing errors.

Scenario 2.

Now the words have length 12 so we can transmit

> wps2:=evalf(10^5/12);

or about 8333 of them per second. With the check digit, as we saw, we

can detect any single error or any odd number of errors in a received word.

Be careful in thinking about this, though -- detecting error(s) just means that

we can tell the received word was not a correct codeword. It doesn't mean

that those errors can be corrected . In this case, in fact, they can't be.

As we saw,

prob of exactly one error in a received word =

prob of exactly two errors = , ...

prob of exactly t errors =

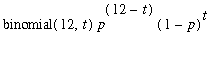
The probability of having an undetectable error is then the same as the probability

of some even number of errors, which is the sum

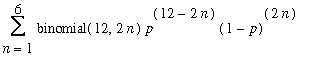
To compute this in Maple, we can use the sum command:

> undetectable2:=sum(binomial(12,2*n)*p^(12-2*n)*(1-p)^(2*n),n=1..6);

(One observation here: The terms in this sum after the first are much smaller in

magnitude than the first one -- more errors in a word are less likely than fewer

errors for this value of p . If we ignore all the terms with n > 1, and just consider

the probability of 2 errors, the result is very close to the one above:

> approxundetectable2:=binomial(12,2)*p^10*(1-p)^2;

-- close!!) Using the better decimal value, this means that we will have

> wps2*undetectable2;

undetectable errors per second. This means that we get an undetectable error about

once every:

> 1/(wps2*undetectable2);

seconds.

It is important to realize that in this scenario we also have detectable errors

that cannot be corrected. These are errors that we know happened, but that

we cannot fix. The probability of these is the same as the probability

of some odd number of errors in a received word:

> detectable2:=sum(binomial(12,2*n-1)*p^(12-2*n+1)*(1-p)^(2*n-1),n=1..6);

> detectable2*wps2;

So there are still about 99 errors per second that we know about but can't

do anything about except to ask that word to be retransmitted.

Finally, Scenario 3.

Here we have a (15,11,3) code. Any single error in a received word can be detected

by "nearest-neighbor" decoding. We are also given that if >=2 errors happen, then

the result will be decoded incorrectly. The question is: how often do we expect

to get an incorrectly decoded word? We have

> wps3:=evalf(10^5/15);

or about 6667 words per second transmitted. The probability of zero or one error

is

> correctable3:=p^15+binomial(15,1)*p^14*(1-p);

> incorrectlydecoded3:=1-correctable3;

So we get on average:

> wps3*incorrectlydecoded3;

incorrectly decoded words per second, or about one every

> 1/(wps3*incorrectlydecoded3);

seconds, or about one every 1.4 seconds.

Comparison of the 3 Scenarios

Efficiency: The more check bits we include, the less efficient the system

is -- we are including more redundant information and transmitting fewer

total words per second -- 10000 words vs. 8333 vs. 6667 per second.

Reliability: Clearly either Scenario 2 or Scenario 3 is more reliable than

Scenario 1, since we cannot tell at all when errors happen in Scenario 1.

In Scenario 2 we know when most of the errors happen (i.e. all but the

even numbers of errors), but there are still about 100 words per second

that have errors. To get the correct message across, we would probably

need to ask the transmitter to send those words again, further reducing

efficiency. Even doing that, we still have an undetected error about once

every 1.8 seconds. In Scenario 3, all but about 1 word every 1.4 seconds

are received and decoded correctly.

So our conclusion is that Scenario 3 is far more reliable than Scenario 2.

To be fair, we should note that there are situations where the efficiency might

outweigh reliability as a criterion -- for example if the information was not

especially "sensitive" to errors -- the fact that 100 out of 10000 were incorrect

(or that 1.8 out of 8333 were undetectably incorrect) might not actually

be a big problem.

B)

1) By the definition, d(x,y) = |{ i : }|, which is an integer >= 0.

It is equal to zero if and only if the set of i for which

is empty, which is equivalent to saying that x = y.

2) d(x,y) = |{ i : }| = |{ i : }| = d(y,x)

3) First proof: computing the Hamming distances here amounts to

counting the number of differences between x,y, between x,z

and between y,z. That can be done by scanning the words

one position (or bit) at a time and analyzing the possibilities:

If , then we add a 0 into the total for d(x,y) for the ith

bit. In d(x,z) + d(z,y), we add in 1 + 1 = 2 if and

and we add in 0 + 0 if = = . Either way the term we added

into d(x,y) is less than or equal to the term we added into

d(x,z) + d(z,y).

If , then we add a 1 into the total for d(x,y). In this

case, either and , or else and

(since each position can only be either a 0 or 1).

Hence we add 0 + 1 or 1 + 0 into d(x,z) + d(z,y). Either way

again, the term we added into d(x,y) is less than or equal to the term

we added into d(x,z) + d(z,y).

Since all of this is true for each i, after adding up the whole

totals: d(x,y) <= d(x,z) + d(z,y).

Second proof (more "elegant"). Let's introduce names for the

sets of locations where each pair of words differ: Let

A = { i : }

B = { i : }

C = { i : }

Then A is a subset of B union C (since if , then either

or ). Hence d(x,y) = |A| <= |B| + |C| = d(x,z) + d(y,z).