MATH 392 -- Seminar in Computational Commutative Algebra 

October 16, 2006 

 

More on the geometry of envelopes of families of curves 

 

Consider the family of normal lines to the parabola   

(A normal line is a line passing through a point on the parabola,  

perpendicular to the tangent line of the parabola at that point.) 

 

Since at a point t, t^2-ton the parabola, the  

equation of the normal line will be  

Clearing denominators we have 

 

   F(x, y, t) = (2*t-1)(y-t^2+t)+x-t 

 

is the function of three variables defining the family of normal  

lines.   

 

> with(Groebner); -1; with(plots); -1
 

> F := (2*t-1)*(y-t^2+t)+x-t; 1
 

(2*t-1)*(y-t^2+t)+x-t 

>
 

There are several ways to visualize this, either by using  tas an  

"animation variable" as we saw in problem II on the Midterm Problem 

Set, or alternatively by considering the variety   V = V(F(x, y, t)) 

in real^3.     

 

In the Midterm Problem Set, we introduced the envelope of the  

family by saying we wanted to produce a curve that was 

tangent to the curves in the family.  This is useful as an 

intuitive way to visualize the envelope, but it is somewhat  

imprecise for several reasons: 

 

  1.  The curves in a family can intersect the envelope at some 

       points where they are tangent to the envelope, but at 

       other points too, where they are not tangent to the envelope. 

 

  2.  The envelope curve itself can have singular points such 

       as cusp points, where it is not clear what saying 

       another curve is tangent to the envelope should mean.   

 

So a somewhat better way to think of the equations 

 

    F(x, y, t) = 0 

    diff(F(x, y, t), t) = 0 

 

which appear in the definition of the envelope is that they define 

a subset (usually a curve) on the surface   

V = V(F(x, y, t)) 

in real^3called the "apparent contour" -- the set of points where 

the tangent plane to V is vertical.  When we eliminate the variable t 

to get the envelope equation, we are finding the projection of  

the apparent contour into the xy - plane. 

 

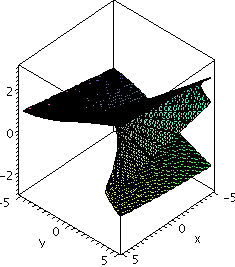
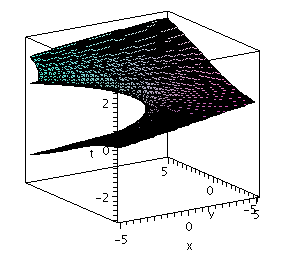
Here are two implicit plots of the surface  V  for the family  

of normal lines to the parabola,  from two different points of view,  

showing where the envelope and the apparent contour of the surface  

come from.  Here is what to look for in these:   

 

  *  In the first one, look for a "lower fold" of the surface giving  

     points on the apparent contour with  `*`(0, see*the*x-axis*scale) < x; 1 

  *  In the second, look for an "upper fold" giving points on the apparent  

     contour with  x < 0; -1 

>
 

> implicitplot3d(F, x = -5 .. 5, y = -5 .. 5, t = -3 .. 3, grid = ([40, 40, 40]), axes = boxed); 1
implicitplot3d(F, x = -5 .. 5, y = -5 .. 5, t = -3 .. 3, grid = ([40, 40, 40]), axes = boxed); 1
 

Plot 

> implicitplot3d(F, x = -5 .. 5, y = -5 .. 5, t = -3 .. 3, grid = ([40, 40, 40]), axes = boxed); 1
implicitplot3d(F, x = -5 .. 5, y = -5 .. 5, t = -3 .. 3, grid = ([40, 40, 40]), axes = boxed); 1
 

Plot 

 

>
 

We can find the equation of the apparent countour or envelope of the family 

by using a lex Grobner basis (to eliminate  tbetween the equations  F(x, y, t) = 0 

and as discussed in the Midterm Problem Set (and Chapter 3, section 4 

in the text).   

> B := Basis([F, diff(F, t)], plex(t, x, y)); 1
 

[-16*y^3+27*x^2+12*y^2-27*x-3*y+7, 4*t*y+3*x-2*y-t-1, 8*y^2+18*x*t-9*x-4*y-9*t+5, -y+3*t^2-3*t+1]
[-16*y^3+27*x^2+12*y^2-27*x-3*y+7, 4*t*y+3*x-2*y-t-1, 8*y^2+18*x*t-9*x-4*y-9*t+5, -y+3*t^2-3*t+1] 

> nops(B); 1
 

4 

The first element of the Grobner basis defines the envelope (projection of the  

apparent contour): 

> B[1]; 1
 

-16*y^3+27*x^2+12*y^2-27*x-3*y+7 

The other elements of the Grobner basis look like this: 

> collect(B[2], t); 1; collect(B[3], t); 1
 

(-1+4*y)*t-1+3*x-2*y 

(-9+18*x)*t+8*y^2+5-9*x-4*y 

> collect(B[4], t); 1
 

-y+3*t^2-3*t+1 

Here is an animated display showing  

 

   * the lines in the family of normal lines (in blue) 

   * the envelope (in red) 

   * the parabola (in black) 

 

> Aplot := animate(implicitplot, [F, x = -5 .. 5, y = -5 .. 5, color = blue], t = -1 .. 2, frames = 40); -1
Aplot := animate(implicitplot, [F, x = -5 .. 5, y = -5 .. 5, color = blue], t = -1 .. 2, frames = 40); -1
 

> Cplot := plot([t, t^2-t, t = -3 .. 3], color = black); -1
 

> Eplot := implicitplot(B[1], x = -5 .. 5, y = -1 .. 5, grid = ([200, 200])); -1
 

> display(Eplot, Aplot, Cplot, view = ([-5 .. 5, -1 .. 5]), axes = boxed, scaling = constrained); 1
display(Eplot, Aplot, Cplot, view = ([-5 .. 5, -1 .. 5]), axes = boxed, scaling = constrained); 1
 

Plot 

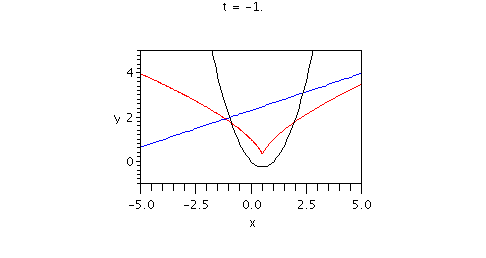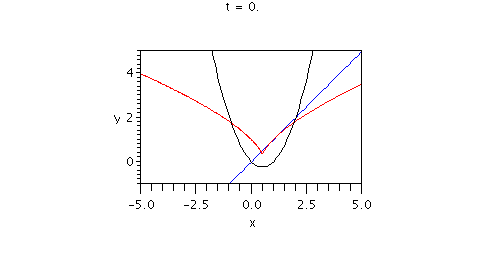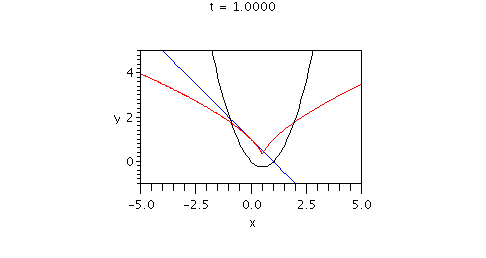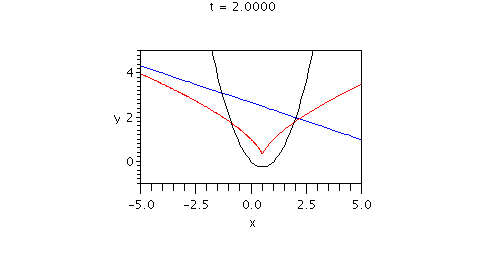
Note that in this case the envelope curve does apparently have a cusp 

point.  We can find the coordinates by solving the equations 

 

    point is on the envelope) 

    diff(B[1], x) = 0(tangent line to the envelope not well-defined) 

    diff(B[2], y) = 0 

> Basis([B[1], diff(B[1], x), diff(B[1], y)], plex(x, y)); 1
 

[16*y^2-8*y+1, 2*x-1] 

>
 

There is actually just one point in the variety defined here:   

which is where the cusp point is located.  Note that this point is also 

where "special behavior" of the Grobner basis  B  occurs -- It's exactly 

that point where the Grobner basis polynomials  B[2] and B[3]  become  

0 for all  t.