MATH 392 -- Seminar in Computational Commutative Algebra 

Lab 2/Problem Set 5  Solutions 

 

> with(Groebner);
 

 

[Basis, FGLM, HilbertDimension, HilbertPolynomial, HilbertSeries, InterReduce, IsProper, IsZeroDimensional, LeadingCoefficient, LeadingMonomial, LeadingTerm, MonomialOrder, MultiplicationMatrix, Norma...
[Basis, FGLM, HilbertDimension, HilbertPolynomial, HilbertSeries, InterReduce, IsProper, IsZeroDimensional, LeadingCoefficient, LeadingMonomial, LeadingTerm, MonomialOrder, MultiplicationMatrix, Norma...
[Basis, FGLM, HilbertDimension, HilbertPolynomial, HilbertSeries, InterReduce, IsProper, IsZeroDimensional, LeadingCoefficient, LeadingMonomial, LeadingTerm, MonomialOrder, MultiplicationMatrix, Norma...
[Basis, FGLM, HilbertDimension, HilbertPolynomial, HilbertSeries, InterReduce, IsProper, IsZeroDimensional, LeadingCoefficient, LeadingMonomial, LeadingTerm, MonomialOrder, MultiplicationMatrix, Norma...
[Basis, FGLM, HilbertDimension, HilbertPolynomial, HilbertSeries, InterReduce, IsProper, IsZeroDimensional, LeadingCoefficient, LeadingMonomial, LeadingTerm, MonomialOrder, MultiplicationMatrix, Norma... 

> Plist:=[x^2*y + x^2 + 1, x^3 + x*y + 2];
 

[x^2*y+x^2+1, x^3+x*y+2] 

>
 

> B:=Basis(Plist,plex(x,y));
 

[y^4+11*y^2+10*y+5+6*y^3, 2*x+y^3+4*y^2+2*y+1] 

>
 

1.  <LT(I)> = <x,y^4>.  The monomial ideal <LT(f_1),LT(f_2)> = <x^2y, x^3> is  

contained in this. 

> f := (x^4*y+x^2*y^3)*Plist[1]+y^2*Plist[2]; 1
 

(x^4*y+x^2*y^3)*(x^2*y+x^2+1)+y^2*(x^3+x*y+2) 

2.   

> NormalForm(f, B, plex(x, y)); 1
 

0 

3.  x has been eliminated from the first equation, so we can solve that, 

substitute back for y in the second, and solve for x. 

 

4. 

> yroots:=[fsolve(B[1]=0,y,complex)];
 

[-3.618033989, -1.381966011, -.5000000000-.8660254038*I, -.5000000000+.8660254038*I]
[-3.618033989, -1.381966011, -.5000000000-.8660254038*I, -.5000000000+.8660254038*I] 

> for i to nops(yroots) do
   Bs:=subs(y=yroots[i],B);
   solve(Bs[2],x);
end do;
 

[0., 2*x-1.236067958] 

.6180339790 

[0.1e-7, 2*x+3.236067978] 

-1.618033989 

[0.+0.1402961154e-9*I, 2*x+(-1.000000000+1.732050807*I)] 

.5000000000-.8660254035*I 

[0.-0.1402961154e-9*I, 2*x+(-1.000000000-1.732050807*I)] 

.5000000000+.8660254035*I 

5.  Same idea, but y is eliminated from the first equation: 

> Basis(Plist,plex(y,x));
 

[x^4-x^2+2*x-1, 2*x^3+x^2+y-2*x+4] 

6.  The grevlex Groebner basis does not have the same elimination  

property (also contains 3 polynomials) 

> Bgrev:=Basis(Plist,tdeg(x,y));
 

[-3-y^2-5*y+4*x+2*x*y, x^2-3-y^2-4*y+2*x, 2*x+y^3+4*y^2+2*y+1]
[-3-y^2-5*y+4*x+2*x*y, x^2-3-y^2-4*y+2*x, 2*x+y^3+4*y^2+2*y+1] 

> for i to 3 do LeadingTerm(Bgrev[i],tdeg(x,y)); end do;
 

2, x*y 

1, x^2 

1, y^3 

>
 

Book problems: 

 

2. 

> PL2 := [x*z-y, x*y+2*z^2, y-z]; 1
 

[x*z-y, x*y+2*z^2, y-z] 

> B := Basis(PL2, tdeg(x, y, z)); 1
 

[y-z, 2*z^2+z, x*z-z] 

> NormalForm(x^3*z-2*y^2, B, tdeg(x, y, z)); 1
 

2*z 

remainder is not zero, so the given f is not in the ideal. 

 

3. 

> PL3 := [x^2+y^2+z^2-1, x^2+y^2+z^2-2*x, 2*x-3*y-z]; 1
 

[x^2+y^2+z^2-1, x^2+y^2+z^2-2*x, 2*x-3*y-z] 

> B3 := Basis(PL3, plex(x, y, z)); 1
 

[40*z^2-8*z-23, 3*y+z-1, 2*x-1] 

> zroots := fsolve(B3[1], z, complex); 1
 

-.6648529270, .8648529270 

> B3s := subs(z = zroots[1], B3); 1
 

[0., 3*y-1.664852927, 2*x-1] 

> solve(B3s[2], y); 1; solve(B3s[3], x); 1
 

.5549509757 

1/2 

>
 

> B3s := subs(z = zroots[2], B3); 1
 

[-0.1e-7, 3*y-.1351470730, 2*x-1] 

> solve(B3s[2], y); 1; solve(B3s[3], x); 1
 

0.4504902433e-1 

1/2 

>
 

>
 

8. 

> plot3d([(2+cos(t))*cos(u),(2+cos(t))*sin(u),sin(t)],t=0..2*Pi,u=0..2*Pi);
 

Plot 

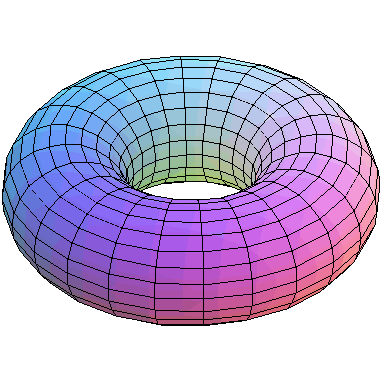
> Id:=[x-(2+ct)*cu,y-(2+ct)*su,z-st,ct^2+st^2-1,cu^2+su^2-1];
 

[x-(2+ct)*cu, y-(2+ct)*su, z-st, ct^2+st^2-1, cu^2+su^2-1] 

> B8:=Basis(Id,plex(ct,st,cu,su,x,y,z));
 

[x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9, 4*su*z^2+x^2*y+y^3+y*z^2+12*su-13*y, 4*su*x^2+4*su*y^2-x^2*y-y^3-y*z^2-3*y, 4*cu*z^2+x^3+x*y^2+z^2*x+12*cu-13*x, -su*x+cu*y, 4*su*y+4*...
[x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9, 4*su*z^2+x^2*y+y^3+y*z^2+12*su-13*y, 4*su*x^2+4*su*y^2-x^2*y-y^3-y*z^2-3*y, 4*cu*z^2+x^3+x*y^2+z^2*x+12*cu-13*x, -su*x+cu*y, 4*su*y+4*...
[x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9, 4*su*z^2+x^2*y+y^3+y*z^2+12*su-13*y, 4*su*x^2+4*su*y^2-x^2*y-y^3-y*z^2-3*y, 4*cu*z^2+x^3+x*y^2+z^2*x+12*cu-13*x, -su*x+cu*y, 4*su*y+4*...
[x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9, 4*su*z^2+x^2*y+y^3+y*z^2+12*su-13*y, 4*su*x^2+4*su*y^2-x^2*y-y^3-y*z^2-3*y, 4*cu*z^2+x^3+x*y^2+z^2*x+12*cu-13*x, -su*x+cu*y, 4*su*y+4*...
[x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9, 4*su*z^2+x^2*y+y^3+y*z^2+12*su-13*y, 4*su*x^2+4*su*y^2-x^2*y-y^3-y*z^2-3*y, 4*cu*z^2+x^3+x*y^2+z^2*x+12*cu-13*x, -su*x+cu*y, 4*su*y+4*...
[x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9, 4*su*z^2+x^2*y+y^3+y*z^2+12*su-13*y, 4*su*x^2+4*su*y^2-x^2*y-y^3-y*z^2-3*y, 4*cu*z^2+x^3+x*y^2+z^2*x+12*cu-13*x, -su*x+cu*y, 4*su*y+4*... 

> B8[1]; 1
 

x^4+2*x^2*y^2+2*x^2*z^2+y^4+2*y^2*z^2+z^4-10*x^2-10*y^2+6*z^2+9 

> expand(cos(3*t), trig), expand(sin(3*t), trig); 1
 

4*cos(t)^3-3*cos(t), 4*sin(t)*cos(t)^2-sin(t) 

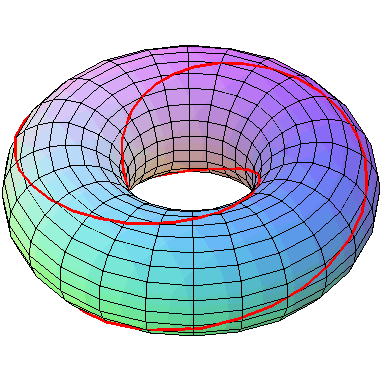
9.   The torus knot: 

> PLK := [x-(2+a^2-b^2)*(4*a^3-3*a), y-(2+a^2-b^2)*(4*b*a^2-b), z-2*a*b, a^2+b^2-1]; 1
PLK := [x-(2+a^2-b^2)*(4*a^3-3*a), y-(2+a^2-b^2)*(4*b*a^2-b), z-2*a*b, a^2+b^2-1]; 1
 

[x-(2+a^2-b^2)*(4*a^3-3*a), y-(2+a^2-b^2)*(4*b*a^2-b), z-2*a*b, a^2+b^2-1]
[x-(2+a^2-b^2)*(4*a^3-3*a), y-(2+a^2-b^2)*(4*b*a^2-b), z-2*a*b, a^2+b^2-1] 

> B9 := Basis(PLK, plex(a, b, x, y, z)); 1
 

[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*...
[72*z^8+64*z^4*y^2+9*z^6+4*y^4-76*y^2*z^2-162*z^4-4*y^2+81*z^2+16*z^10, 64*y*z^6-96*x*z^5+8*y^3*z^2-88*z^4*y+67*x*z^3-6*y*z^2+16*z^7*x-3*x*z-2*y^3+2*y, 8*y*z^4*x-16*z^9-42*y*z^2*x-80*z^7+2*x*y-32*z^3*... 

> NormalForm(B8[1], B9, plex(a, b, x, y, z)); 1
 

0 

This says the curve K lies on the torus T.  Here is a plot showing that:
 

> TP := plot3d([(2+cos(t))*cos(u), (2+cos(t))*sin(u), sin(t)], t = 0 .. 2*Pi, u = 0 .. 2*Pi); -1
TP := plot3d([(2+cos(t))*cos(u), (2+cos(t))*sin(u), sin(t)], t = 0 .. 2*Pi, u = 0 .. 2*Pi); -1
 

> KP := spacecurve([(2+cos(2*s))*cos(3*s), (2+cos(2*s))*sin(3*s), sin(2*s)], s = 0 .. 2*Pi, numpoints = 100, color = red, thickness = 2); -1
KP := spacecurve([(2+cos(2*s))*cos(3*s), (2+cos(2*s))*sin(3*s), sin(2*s)], s = 0 .. 2*Pi, numpoints = 100, color = red, thickness = 2); -1
 

> with(plots); -1
 

> display(TP, KP, scaling = CONSTRAINED); 1
 

Plot 

10.   We want to maximize the (squared) distance  f  from the  

point (1,1,1), at the poinst on the surface  V(g)  using Lagrange Multipliers 

> f := (x-1)^2+(y-1)^2+(z-1)^2; 1
 

(x-1)^2+(y-1)^2+(z-1)^2 

> g := x^4+y^2+z^2-1; 1
 

x^4+y^2+z^2-1 

> PL10 := [(diff(f, x))-lambda*(diff(g, x)), (diff(f, y))-lambda*(diff(g, y)), (diff(f, z))-lambda*(diff(g, z)), g]; 1
PL10 := [(diff(f, x))-lambda*(diff(g, x)), (diff(f, y))-lambda*(diff(g, y)), (diff(f, z))-lambda*(diff(g, z)), g]; 1
 

[2*x-2-4*lambda*x^3, 2*y-2-2*lambda*y, 2*z-2-2*lambda*z, x^4+y^2+z^2-1] 

> B10 := Basis(PL10, plex(lambda, x, y, z)); 1
 

[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176...
[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176...
[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176...
[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176...
[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176...
[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176...
[64*z^10+176*z^4+4*z^2+32*z-172*z^3-8+96*z^7+232*z^5-471*z^6+304*z^8-256*z^9, y-z, 4*x-192*z^9+54*z^4+252*z^2+156*z-840*z^3-68-400*z^7+1285*z^5-896*z^6+640*z^8, 8*lambda-172*z^2+4*z+96*z^6+232*z^4+176... 

> zrts := fsolve(B10[1], z, complex); 1
 

-.7364766946-0.8754698995e-2*I, -.7364766946+0.8754698995e-2*I, -.6235204055, .4955573659-.1400771672*I, .4955573659+.1400771672*I, .6348187101, 1.000035403-.6475570597*I, 1.000035403+.6475570597*I, 1...
-.7364766946-0.8754698995e-2*I, -.7364766946+0.8754698995e-2*I, -.6235204055, .4955573659-.1400771672*I, .4955573659+.1400771672*I, .6348187101, 1.000035403-.6475570597*I, 1.000035403+.6475570597*I, 1...
-.7364766946-0.8754698995e-2*I, -.7364766946+0.8754698995e-2*I, -.6235204055, .4955573659-.1400771672*I, .4955573659+.1400771672*I, .6348187101, 1.000035403-.6475570597*I, 1.000035403+.6475570597*I, 1...
-.7364766946-0.8754698995e-2*I, -.7364766946+0.8754698995e-2*I, -.6235204055, .4955573659-.1400771672*I, .4955573659+.1400771672*I, .6348187101, 1.000035403-.6475570597*I, 1.000035403+.6475570597*I, 1...
-.7364766946-0.8754698995e-2*I, -.7364766946+0.8754698995e-2*I, -.6235204055, .4955573659-.1400771672*I, .4955573659+.1400771672*I, .6348187101, 1.000035403-.6475570597*I, 1.000035403+.6475570597*I, 1...
-.7364766946-0.8754698995e-2*I, -.7364766946+0.8754698995e-2*I, -.6235204055, .4955573659-.1400771672*I, .4955573659+.1400771672*I, .6348187101, 1.000035403-.6475570597*I, 1.000035403+.6475570597*I, 1... 

> B10s := subs(z = zrts[3], B10); 1
 

[0.5e-8, y+.6235204055, 4*x+2.74704305, 8*lambda-20.83037400] 

> zrts[3]; 1; solve(B10s[2], y); 1; solve(B10s[3], x); 1
 

-.6235204055 

-.6235204055 

-.6867607625 

>
 

> B10s := subs(z = zrts[6], B10); 1
 

[0.2e-8, y-.6348187101, 4*x-2.65470491, 8*lambda+4.602023047] 

> zrts[6]; 1; solve(B10s[2], y); 1; solve(B10s[3], x); 1
 

.6348187101 

.6348187101 

.6636762275 

Clearly the point with all positive coordinates is closer to (1,1,1) than the point 

with all negative coordinates. 

>