>

 

MATH 392 -- Seminar in Computational Commutative Algebra 

Another "black box" Gr"obner basis calculation. 

We saw in the lab last Friday that lex Gr"obner bases 

apparently can eliminate variables and produce elements 

of a polynomial ideal that contain only some of the  

variables present in the original polynomials (if there 

are such).  One place where this might be useful is when 

we want to find implicit equations of parametrically defined 

curves or surfaces.  Here is one such example, which is  

even a case where the parametrization involves trig functions: 

    x = sin(t) cos^3(t) 

    y = sin^2(t) cos(t) 

in the plane.   

>

 

>	plot([2*sin(t)*cos(t)^3,sin(t)^2*cos(t),t=0..2*Pi]);

 

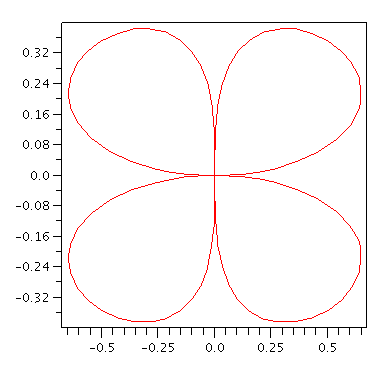
We introduce variables  s  for sin(t),  c for cos(t), 

and add the algebraic relation  s^2 + c^2  -  1 = 0  for all t. 

Let's see what happens if we compute a lex Gr"obner basis 

for the ideal  

   < x - sc^3,  y - s^2c, s^2 + c^2 - 1> 

(lex order with   s > c > x > y  to try to eliminate s, c ) 

>	with(Groebner);

 

>	Id:=[x-s*c^3,y-s^2*c,s^2+c^2-1];

 

>	B:=Basis(Id,plex(s,c,x,y));

 

>

 

Note that the first element of the Gr"obner basis does contain only x,y 

terms, as we hoped!   The variety defined by that polynomial also looks 

right! 

>	with(plots):

 

>	implicitplot(B[1],x=-1..1,y=-1..1,grid=[200,200]);

 

>
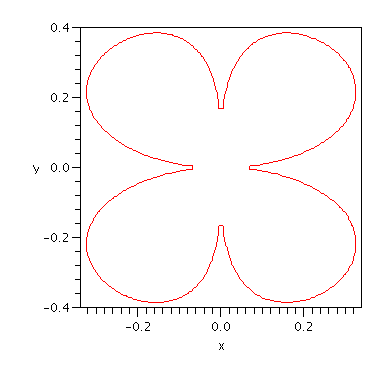