MATH 136 -- Advanced Placement Calculus 

An Euler's Method Example 

November 18, 2009 

 

We study the approximate solution of  `/`(`*`(dy), `*`(dx)) = `+`(`*`(`^`(x, 2)), `*`(`^`(y, 2))) with initial  

condition  y(0) = 1.  We do 10 steps of Euler's method with  

`*`(Delta, `*`(x)) = .1  to approximate the solution at  x  between 0 and 1.
The Maple commands below execute the Euler's Method iteration 

we discussed: 

 

           x[i] = `+`(x[`+`(i, `-`(1))], `Δx`) 

         

           y[i] = `+`(y[`+`(i, `-`(1))], `*`(f(x[`+`(i, `-`(1))], y[`+`(i, `-`(1))]), `*`(`Δx`))) 

 

for the slope function  starting from  x[0] = 0, y[0] = 1; -1 

> with(DEtools):
 

> with(plots):
 

> xlist[0]:=0; ylist[0]:=1;
 

 

0
1 (1)
 

> for i to 10 do
  xlist[i]:=xlist[i-1]+.1;
  ylist[i]:= eval(ylist[i-1]+(xlist[i-1]^2+ylist[i-1]^2)*(.1));
end do;
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.1
1.1
.2
1.222
.3
1.3753284
.4
1.573481221
.5
1.837065536
.6
2.199546514
.7
2.719347001
.8
3.507831812
.9
4.802320214
1.0
7.189548158 (2)
 

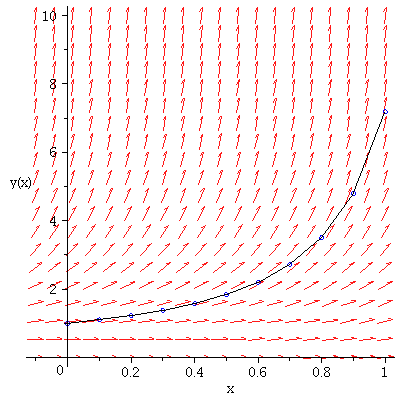
> DirField:=dfieldplot(diff(y(x),x)= x^2 + y(x)^2,[y(x)],x=-.1..1,y=0..10):
 

> Pts:=plot([seq([xlist[i],ylist[i]],i=0..10)],style=point,symbol=circle,color=blue):
 

> Lines:=plot([seq([xlist[i],ylist[i]],i=0..10)],color=black):
 

> display(DirField,Pts,Lines);
 

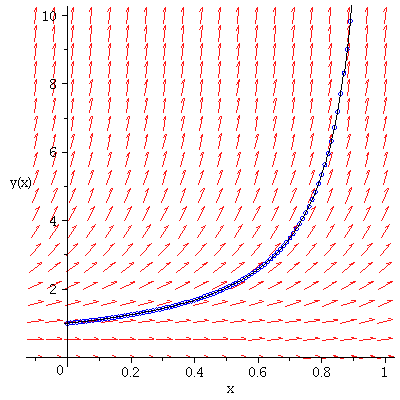
Plot_2d
 

We would get a better approximation with smaller `*`(Delta, `*`(x)).  For instance, with  .01: 

> xlist[0]:=0: ylist[0]:=1:
 

> for i to 100 do
  xlist[i]:=xlist[i-1]+.01;
  ylist[i]:= eval(ylist[i-1]+(xlist[i-1]^2+ylist[i-1]^2)*(.01));
end do:
 

> Pts:=plot([seq([xlist[i],ylist[i]],i=0..100)],style=point,symbol=circle,color=blue):
 

> Lines:=plot([seq([xlist[i],ylist[i]],i=0..100)],color=black):
 

> display(DirField,Pts,Lines);
 

Plot_2d
 

>