MATH 376 -- Probability and Statistics II

Type II Error Probabilities for a large-sample lower-tail Z-test

March 22, 2006

We consider testing for value of a proportion.  Say the null

hypothesis is  :   p = .3  and the alternative hypothesis is

   :   p < .3.   We will assume   n   is always large enough

so that our general discussions of the large-sample tests applies.

The test statistic is   z = 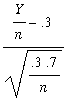  and the rejection region for

an -level test is  RR = { z < z_.05 } = { z < -1.645 }

or  { Y/n < .3 - 1.645  }.

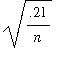Set-up:

>	sigma[1]:=n->sqrt((.3)*(.7)/n);

The normal pdf under the assumption that     is true:

>	f[1]:=n->1/sqrt(2*Pi*sigma[1](n)^2)*exp(-(y-.3)^2/(2*sigma[1](n)^2));

But now suppose that the actual value of   p   is  .24.  We ask:  How likely are

we to make a Type II error with the  = .05-level rejection region given above?

Here's the normal pdf that approximates the distribution with   p = .24:

>	sigma[2]:=n->sqrt((.24)*(.76)/n);

>	f[2]:=n->1/sqrt(2*Pi*sigma[2](n)^2)*exp(-(y-.24)^2/(2*sigma[2](n)^2));

>	RR:=n->.3-1.645*sigma[1](n);

The following plot shows the normal densities for the sampling distribution

of Y/ 100:

    blue plot (shorter normal curve) = if   is true

    red plot (taller normal curve) = if   is false and actual  p = .24

The vertical black line is plotted at the value .2246 (the upper edge of the RR taking

n = 100. )

>

RR(100);

>	Dists:=plot([f[1](100),f[2](100)],y=0..0.5,color=[blue,red]):

>	RRPlot:=plot([RR(100),t,t=0..10],color=black):

>	with(plots):

>	display(Dists,RRPlot);

The area under the shorter normal curve to the left  of the black line is the probability

of a Type I error:

>	evalf(Int(f[1](100),y=-infinity..RR(100)));

This checks with the desired value    = .05 The area under the taller normal curve to the

right of the black line is the probability of a Type II error (always assuming   p = .24):

>	evalf(Int(f[2](100),y=RR(100)..infinity));

This is certainly unacceptably large!  What can we do to decrease it?  

The answer is:  Increase the sample size(!)  Increasing n decreases the variances of both

distributions (so the pdf's get taller and skinnier) , and moves the cut-off for the RR for the

.05-level test farther to the right.  For instance the picture for n = 500 is:

>

RR(500);

>	Dists:=plot([f[1](500),f[2](500)],y=0..0.5,color=[blue,red]):

>	RRPlot:=plot([RR(500),t,t=0..15],color=black):

>	display(Dists,RRPlot);

>	evalf(Int(f[2](500),y=RR(500)..infinity));

>

So the Type II error probability     has been reduced to .084 by increasing   n   to 500,

while  = .05 still.  In class we showed that   can be reduced to any given value

by taking n sufficiently large.