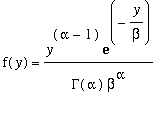MATH 375 -- Probability and Statistics 1

Gamma Distributions

October 29, 2003

Recall that we say   Y   has a Gamma distribution

if its pdf has the form

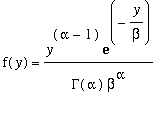   for   y >= 0  (and  0  for y  < 0)

>	read "/home/fac/little/public_html/ProbStat/MaplePackage/MSP.map";

In our Maple package, the Gamma probability density function

is called GammaPDF -- it takes three parameters,

>	GammaPDF(2,3,1.3);

The Gamma distributions include distributions of various shapes,

skewed to different degrees always   to the right.

The Gamma distribution with  is a special case called

the exponential distribution.   We looked at these already in an

example from class on Wednesday, 10/22.  The exponential

pdf is always decreasing (a decaying exponential)

>	plot(y->GammaPDF(1,2,y),0..10);

When   ,  the pdf has a local maximum at a positive   y.

For instance, with ,  we have distributions like the following.  

Increasing the parameter   stretches horizontally (hence shrinks

vertically too to keep the total area = 1).

>	plot(y->GammaPDF(2,1,y),0..20);

>	plot(y->GammaPDF(2,3,y),0..20);

With   , ,  note that the peak has shifted to the right compared to

and the overall distribution is more symmetrical.

>	plot(y->GammaPDF(4,1,y),0..30);

>	plot(y->GammaPDF(4,3,y),0..30);

Finally, with ,  we get something quite symmetrical.  

>	plot(y->GammaPDF(50,1,y),0..120);

The mean here is , and the variance is .  For comparison,

here is the corresponding normal pdf plotted together with the Gamma pdf.

The Gamma pdf is skewed to the right compared to the normal.

>	plot([y->NormalPDF(50,sqrt(50),y),y->GammaPDF(50,1,y)],20..120,color=[red,black]);

>