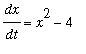
MATH 304 -- Ordinary Differential Equations
Equilibrium points for non-linear systems
November 8, 2004
The first-order system
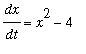
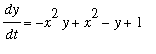
has two equlibrium points: (2,1) and (-2,1)
Let's use Maple's phaseportrait command
to plot some solutions to visualize what is
going on:
| > | eqns:={diff(x(t),t)=x(t)^2-4,diff(y(t),t) =-x(t)^2*y(t)+x(t)^2-y(t)+1}; |
![]()
| > | with(DEtools): |
| > | phaseportrait(eqns,[x(t),y(t)],t=0..0.15,[seq(seq([x(0)=i,y(0)=j],j=-3..3),i=-3..3)],linecolor=black,arrows=slim); |
![[Maple Plot]](images/ODE1184.gif)
From this evidence it looks like the equlibrium point at (-2,1) is a sink (since all
solutions that start nearby seem to be tending toward that point). On the other
hand, (2,1) is a saddle point (since some solutions approach, but others
tend away from that point).
In fact the linearization of the system at (-2,1) is the 1st order linear system
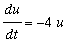 ,
,
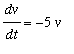 , where
u = x +
2,
v = y
- 1
, where
u = x +
2,
v = y
- 1
which has a sink at ( u,v ) = (0,0). Similarly, at (2,1) we get
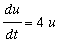 ,
,
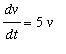 , where
u = x
- 2,
v = y -
1,
, where
u = x
- 2,
v = y -
1,
which has a saddle point at ( u,v ) = (0,0).
| > |