MATH 304 -- Ordinary Differential Equations

A Reduction of Order example.

October 19, 2000

For the linear second order ODE

= 0 (a special case of Hermite's equation )

we derived a polynomial solution . Then the Reduction

of Order formula gives a second solution in the form:

=

This function cannot be expressed in terms of elementary functions, but

we can look at a Taylor series, for instance. To get the terms out to degree

d for instance, we would want to take the Taylor polynomial of degree

d - 1 for , integrate it, and multiply by 1 - 2 , keeping

only terms of degree d or less:

For instance the Taylor polynomial of degree 6 for the second solution is:

> TP6:=convert(taylor(exp(x^2)/(1-2*x^2)^2,x=0,7),polynom);

> expand((1-2*x^2)*int(TP6,x));

> y := expand((1-2*x^2)*int(TP6,x))+277*x^9/21;

(and ignore the term of degree 9). This is only an approximation to the actual solution, but

note:

> expand(diff(y,x$2) - 2*x*diff(y,x) + 4*y);

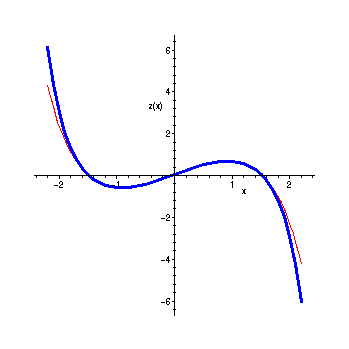
So the Taylor polynomial solves the ODE " modulo " and should agree closely with

the actual solution for x near 0.

> TPlot:=plot(y,x=-2.2..2.2):

> with(DEtools): with(plots):

> SolPlot:=DEplot(diff(z(x),x$2) - 2*x*diff(z(x),x) + 4*z(x),z(x),x=-2.2..2.2,[[z(0)=0,D(z)(0)=1]],linecolor=blue,stepsize=.1):

> display({TPlot,SolPlot});

>