MATH 304 -- Ordinary Differential Equations

A 1st Order Autonomous System

October 31, 2000

We consider the first order autonomous system of ODE:

which has three critical points: ( x,y ) = (0,0), (1,0), (-1,0)

> with(DEtools): with(plots):

The following plot shows several trajectories of this system in the xy phase plane ( t, the

independent variable, is not shown )

> phaseportrait([D(x)(t)=y(t),D(y)(t)=x(t)-x(t)^3],[x(t),y(t)],t=0..5,[[x(0)=-.7,y(0)=.2],[x(0)=.8,y(0)=-.1],[x(0)=.6,y(0)=-.4],[x(0)=.6,y(0)=-.6]],stepsize=.01,linecolor=black);

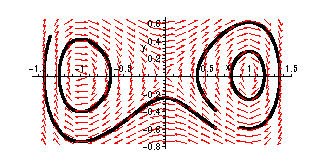
From this plot of the direction field, and the trajectories (flow lines), it appears

that (0,0) is a saddle point (unstable), and (1,0), (-1,0) are centers (stable).

The corresponding functions

> phaseportrait([D(x)(t)=y(t),D(y)(t)=x(t)-x(t)^3],[x(t),y(t)],t=0..10,[[x(0)=-.7,y(0)=.2]],stepsize=.01,linecolor=black,scene=[t,x(t)]);

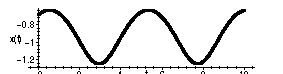
and

> phaseportrait([D(x)(t)=y(t),D(y)(t)=x(t)-x(t)^3],[x(t),y(t)],t=0..10,[[x(0)=-.7,y(0)=.2]],stepsize=.01,linecolor=black,scene=[t,y(t)]);

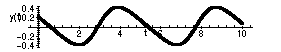
for the solution with initial conditions and y( 0 ) = .2. Note: these

are evidently periodic functions of t.

The associated phase plane equation is the ODE:

This is a separable equation, and the solutions can be found easily in implicit form:

> implicitplot({seq(y^2 - x^2 + x^4/2 + c/10,c=-4..4)},x=-2..2,y=-2..2,grid=[50,50]);

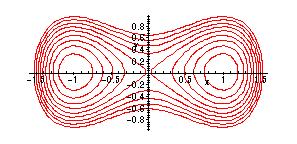
Note the resemblance with the plot above! These curves are the integral curves

of the system. All trajectories lie on one of these.

>