General Information

Mathematics 304 -- Ordinary Differential Equations

Prof. Little

TR 2 - 3:15 pm

Prerequisites: MATH 242 (Principles of Analysis), MATH 244 (Linear Algebra)

Note: This course is part of a new year-long linked sequence satisfying the

full-year requirement for the Mathematics major: MATH 304, 373 (ODE, PDE).

Students who have taken MATH 373, 374 (Applied Mathematics 1,2) may

sign up for this course, but not the second semester.

A Taste of the Subject

Differential equations are relationships between rates of change of quantities and the

quantities themselves. Many of the basic models of physical and biological processes

can be stated this way, so differential equations give mathematical tools for understanding

the real world. Here is an example: Consider the problem of determining what the

temperature will be in a building, provided we know the outside temperature, the

thermal properties of the material of the building, and also how much heating or

air conditioning is being applied within the building. For simplicity, we make the

following assumptions:

- there is only one "heating zone" and the temperature is uniform throughout the

building (but it can change with time)

- the air outside of the building is also of uniform temperature (but that can also

change with time)

From a relationship called Newton's Law of Heating and Cooling observed through

experiments, we know that for an object with no internal heating/cooling

- the rate of change of the temperature of an object in a surrouding medium of

uniform temperature is directly proportional to the difference between the object's

temperature and the surrounding temperature

Here we want to consider the building as the object. Writing T(t) for the building

temperature as a function of time and A(t) for the ambient temperature around the

building (also a function of time), Newton's Law of Heating and Cooling would

say that

T '(t) = k(T(t) - A(t))

where k is a constant of proportionality. Its value would depend on the properties

of the building's material. For example, good insulation <=> small k. Do you see why ?

The contribution of the building's furnace and air conditioner adds a second term

H(t) to the right hand side:

T '(t) = k(T(t) - A(t)) + H(t)

This is an example of a first-order ordinary differential equation. The "variable"

in the equation is the function T(t), and solving the equation would mean determining

that function (in some form), given some additional information about the temperature

(e.g. the temperature at time t = 0 ) .

Much of the ODE course will be devoted to different methods for solving ODE's like

this: graphical, numeric, and symbolic. For instance, let t be measured in days, and

let A(t) = be the ambient temperature.

(Think t = 0 <-> July, while t = 182.5 <-> January.)

> A := t -> 10*cos(2*Pi*t)+30*cos(2*Pi*t/365)+50;

> plot(A(t),t=0..365,numpoints = 500);

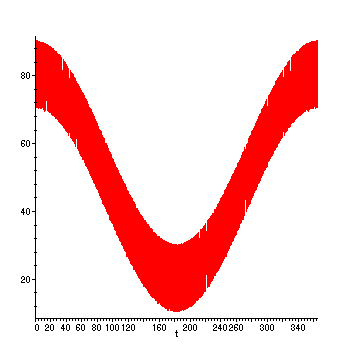
We could ask, for example, How should H(t) be chosen to make the interior temperature

of the building as close as possible to a comfortable constant 70 degrees?

If we take (something like) Holy Cross Physical Plant's method, we could try cranking the heat up to

a constant level for the months November through April, cranking the air conditioning

up to a constant level for the months July and August, and no heating or air conditioning

the rest of the year:

> H := t -> piecewise(t < 60,-.5,t < 120,0,t < 300,1.5,0);

> plot(H(t),t=0..365,y=-3..5);

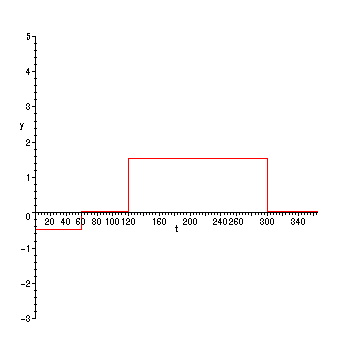
Here is Maple's built-in numerical/graphical method for solving the equation:

> with(DEtools):

> eqn := diff(T(t),t) = (-.05)*(T(t)-A(t)) + H(t);

> DEplot(eqn,T(t),t=0..360,[[T(0)=70]],stepsize=.1,linecolor=blue);

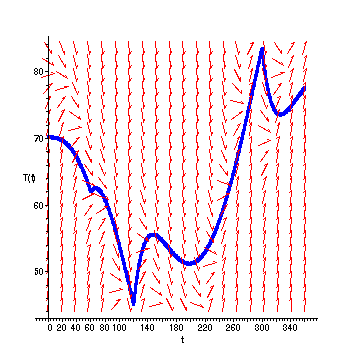
(Getting things balanced by "twiddling" the function H is pretty difficult!) For this equation, because

the form is relatively simple, it is also possible to solve for T(t) symbolically:

> dsolve(eqn,T(t));

We will learn a number of symbolic techniques for solving ODE, including the one that was used here.

We will also learn a number of different applications of ODE to different areas in mathematics and the

sciences.

>