Mathematics 371 -- Numerical Analysis

August 31, 2001

Floating point numbers are provided in hardware in most general-purpose

computers. Some software like Maple also include implementations of

floating point number systems. The default floating point number system in

Maple uses 10 decimal digits and rounds. There is also a system variable

called Digits (capital D) that can be set by you. This allows you to work

with floating point number systems that store more (or fewer) than 10 digits.

Some examples of floating point computations:

Unexpected phenomena can show up in almost any mathematical calculation

done with floating point arithmetic. For example, solving a quadratic equation:

> Digits:=10;

> fsolve(x^2+410.31*x+1,x,complex);

The results from the quadratic formula, using 5 decimal digits:

> Digits:=5;

> (-410.31+sqrt(410.31^2-4*1*1))/2;

> (-410.31-sqrt(410.31^2-4*1*1))/2;

Notice that the root larger in absolute value is correct to 5 decimal digits with rounding.

But the approximation to the small root has a relative error of 310% (that's really bad! )

> abs(-.002437196120 +.01)/abs(-.002437196120);

Similar problems can occur with computations from linear algebra, such

as solving simultaneous systems of linear equations:

> M:=matrix([[67.1,13.01],[175.1,34.0]]);

> with(linalg):

> Digits:=4;

> linsolve(M,[1,0]);

> Digits:=10;

> linsolve(M,[1,0]);

All of these examples show the potential effect of roundoff error in numerical

computation. In this course, we will need to keep an eye on this and analyze

the behavior of our approximation algorithms when they are carried out in

floating point arithmetic.

There are also some more subtle things that can happen here.

The following Maple function computes the 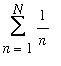sum ( N th partial sum

of the harmonic series), representing each term as a decimal floating point

number (via the built-in evalf function):

> harmonic:=N->add(evalf(1/n),n=1..N);

Mathematically, we know the infinite harmonic series diverges, so the partial sums

grow without bound as .

Here are a few values of harmonic(N):

> harmonic(10^3);

> harmonic(10^4);

> harmonic(10^5);

Seems OK, but there is actually something "funny" going on here. To magnify the

phenomenon and make it show up faster, let's use a smaller number of decimal digits

in our floating point numbers (still rounding):

> Digits:=5;

> harmonic(10^3);

> harmonic(10^4);

> harmonic(10^5);

> harmonic(10^6);

In fact, all larger N will yield this same result ! (Do you see why?) The same

sort of thing would also happen with the default value Digits = 10 but it would

take longer to show up (and also much longer to compute the sums that turn out

to be drastically incorrect, since that happens for larger N ).