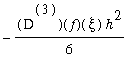MATH 371 -- Numerical Analysis

Numerical Differentiation -- ``the dark side''

October 22, 2001

It's tempting to think that we can get ``super-accurate''

approximate numerical derivatives by taking very small

h , and/or using n -point difference formulas with big n.

From the mathematical point of view, that seems reasonable

for the centered difference formula, for instance, since we know

the error is 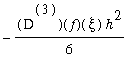, which -> 0 rapidly

as h -> 0.

Let's see what happens, though estimating f '(.2) for

f( x ) = sin( x ) using the centered difference formula with

h progressively smaller: h =

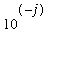
> f:=x->sin(x);

> CD := h -> (f(.2+h) - f(.2-h))/(2*h);

> for j to 9 do lprint(j,CD(10^(-j)),abs(CD(10^(-j))-cos(.2))); end do;

1, .9784339500, .16326278e-2

2, .9800502400, .163378e-4

3, .9800664500, .1278e-6

4, .9800670000, .4222e-6

5, .9800700000, .34222e-5

6, .9801000000, .334222e-4

7, .9800000000, .665778e-4

8, .9800000000, .665778e-4

9, 1.000000000, .199334222e-1

Recall the exact derivative value to 10 decimals is:

> cos(.2);

Our best approximation occurred for j = 3, and then the approximation

started getting worse!? What gives?! This is a case where roundoff error

is spoiling our theoretical error bound. In Maple's default 10-digit floating

point number system, it is reasonable that the computed values of the sin function

have roundoff errors on the order of 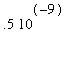Then the smaller h is, the

more severe the round-off effects will be:

> TotalErrorBound:=h->.5e-9/(2*h) + h^2/6;

> for j to 9 do lprint(TotalErrorBound(10^(-j))) end do;

.1666669167e-2

.1669166667e-4

.4166666667e-6

.2501666667e-5

.2500001667e-4

.2500000002e-3

.2500000000e-2

.2500000000e-1

.2500000000

which is quite consistent with our results above(!)