MATH 371 -- Final Problem Set Solutions
December 13, 2001
I A) Using the interpolating polynomial to estimate I' (1.25):
> tlist:=[1.0,1.1,1.2,1.3,1.4];
![]()
> Ilist:=[28.2277,7.2428,-5.9908,4.5260,.29122];
![]()
> with(CurveFitting);
![]()
![]()
> IP:=PolynomialInterpolation(tlist,Ilist,t);
![]()
> subs(t=1.25,diff(IP,t));
![]()
B) Using a free spline to estimate I' (1.25):
> FIS:=Spline(tlist,Ilist,t);
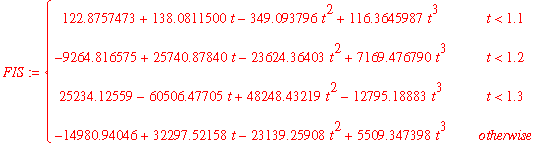
> subs(t=1.25,diff(25234.12559-60506.47705*t+48248.43219*t^2-12795.18883*t^3,t));
![]()
Using a clamped spline, the results are quite similar:
> read "/home/fac/little/public_html/Num01/ClampedSpline.map";
> df0:=(Ilist[2]-Ilist[1])/.1;
![]()
> dfn:=(Ilist[5]-Ilist[4])/.1;
![]()
> CIS:=clampedspline(tlist,Ilist,df0,dfn,t);
![]()
![]()
![]()
![]()
> subs(t=1.25,diff(-28.26636564+18.56297137*t+2253.167001*(-1.2+t)^2-13871.16715*(-1.2+t)^3,t));
![]()
C) The 3-point centered difference formula for the first derivative is
f'(
![]() ) is approximately
) is approximately
![(f(x[0]+h)-f(x[0]-h))/(2*h)](images/FPSSols17.gif) . With the information
. With the information
from the tabulated values, we have essentially only 2 choices for h with
![]() , namely,
h =
.05, and .15. The two approximate values are:
, namely,
h =
.05, and .15. The two approximate values are:
> d1:=(Ilist[5]-Ilist[2])/.3;
![]()
> d2:=(Ilist[4]-Ilist[3])/.1;
![]()
Since the error for the 3-point centered difference is
![]() to extrapolate
to extrapolate
with
h, h/3,
we use:
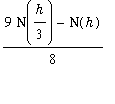
> extrap:=(9*d2-d1)/8;
![]()
which is very close to the result from part A.
To compare these approximations, we can consider the graphs of the various
interpolating functions we have used:
> PPlot:=plot([seq([tlist[j],Ilist[j]],j=1..5)],style=point,color=blue):
> IPlot:=plot(IP,t=1.0..1.4,color=black):
> FSPlot:=plot(FIS,t=1.0..1.4,color=red):
> CSPlot:=plot(CIS,t=1.0..1.4,color=green):
> with(plots):
> display({PPlot,IPlot,FSPlot,CSPlot});
![[Maple Plot]](images/FPSSols24.gif)
Note that in this case the splines are very close, and the interpolating polynomial is
``undershooting'' between 1.2 and 1.3 in preparation for a noticeable "wiggle" between
1.3 and 1.4. The spline interpolants are probably somewhat more reliable for this reason,
but this is not really a clear choice either way.
II A) Incorporating the constant
![]() factor into the integrand, we consider:
factor into the integrand, we consider:
> f:=t->cos(0.6*sin(t))/Pi;
![]()
The error bound for Simpson's Rule involves the fourth derivative of f:
> plot(diff(f(t),t$4),t=0..Pi);
![[Maple Plot]](images/FPSSols27.gif)
So an upper bound for the absolute value of the fourth derivative is .5. The composite
Simpson error bound is then
> errorbound:= (Pi-0)*.5/180*h^4;
![]()
> solve(errorbound=1e-8,h);
![]()
> evalf(Pi/.3271810614e-1);
![]()
n >= 98 -- 99 evaluations
(actually a much smaller number of evaluations also works; as always this
upper bound on the error can be quite a bit larger than the actual error.)
> with(student);
![]()
![]()
![]()
> evalf(simpson(f(t),t=0..Pi,98));
![]()
Note: we also get the required accuracy with a much smaller n
> evalf(simpson(f(t),t=0..Pi,8));
![]()
B) Using the Romberg procedure from class:
> read "/home/fac/little/public_html/Romberg.map";
> Romberg(f,0.0,evalf(Pi),6);
.9999999999
.9126678074, .8835570767
.9120048665, .9117838863, .9136656733
.9120048634, .9120048627, .9120195940, .9119934659
.9120048637, .9120048640, .9120048640, .9120046303, .9120046741
.9120048637, .9120048637, .9120048640, .9120048641, .9120048651, .9120048653
![]()
This method requires 2+1+2+4+8+16 = 33 evaluations of f
(2 in first trapezoidal rule, then one more for the first subdivision,
then 2 more, 4 more, 8 more, 16 more to get 6th row in Romberg
table). Note that the trapezoidal approximations get
accurate very quickly on this example, but the
extrapolated values don't "catch up" so fast because of the error in
the first row.
C) Gaussian 5-point quadrature roots and weights:
> x[5,1]:=-.9061798459:
> x[5,2]:=-.5384693101:
> x[5,3]:=0:
> x[5,4]:=-x[5,2]:
> x[5,5]:=-x[5,1]:
> c[5,1]:=.2369268850:
> c[5,2]:=.4786286705:
> c[5,3]:=.5688888889:
> c[5,4]:=c[5,2]:
> c[5,5]:=c[5,1]:
Because the interval is
![]() instead of [-1,1], we need to use the change
instead of [-1,1], we need to use the change
of variables
x
= (
u
+1)
![]() so
so

> evalf(add(c[5,j]*f((x[5,j]+1)*evalf(Pi)/2),j=1..5)*Pi/2);
![]()
So need to subdivide farther -- take 2 subintervals
![[0, Pi/2]](images/FPSSols41.gif) and
and
![[Pi/2, Pi]](images/FPSSols42.gif)
and use the 5-point formula on each piece:
> firsthalf:=evalf(add(c[5,j]*f((x[5,j]+1)*evalf(Pi)/4),j=1..5)*Pi/4);
![]()
> secondhalf:=evalf(add(c[5,j]*f((x[5,j]+3)*evalf(Pi)/4),j=1..5)*Pi/4);
![]()
> firsthalf+secondhalf;
![]()
In terms of evaluations of f:
* our Simpson calculation based on the error bound used 99 evaluations
(but 9 would actually suffice).
* Romberg used 33 evaluations (but the composite trapezoidal rule with
n = 4 -- 5 evaluations -- also gives the required accuracy), and
* Gaussian Quadrature used 10 evaluations. (Other methods of
subdividing the interval can reduce this a bit too.)
This example shows that it is possible to get much better accuracy than is
predicted by the error bounds in some cases(!)
III.
A) The recurrence relation for the Laguerre polynomials:
> L[0]:=1; L[1]:=1-x;
![]()
![]()
> for n to 3 do L[n+1]:=expand((1+2*n-x)*L[n]-n^2*L[n-1]); end do;
![]()
![]()
![]()
B) The idea is the same as the proof we did in class without the
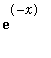 factor in the integrand.
factor in the integrand.
C)
> for i from 0 to 2 do for j from i+1 to 3 do lprint("inner product of L",i,"and L",j,"is", int(L[i]*L[j]*exp(-x),x=0..infinity)); end do: end do:
"inner product of L", 0, "and L", 1, "is", 0
"inner product of L", 0, "and L", 2, "is", 0
"inner product of L", 0, "and L", 3, "is", 0
"inner product of L", 1, "and L", 2, "is", 0
"inner product of L", 1, "and L", 3, "is", 0
"inner product of L", 2, "and L", 3, "is", 0
> read "/home/fac/little/public_html/Num01/Newton.map";
> print(NewtonRaphson);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> f:=x->24-96*x+72*x^2-16*x^3+x^4;
![]()
> plot(f(x),x=0..10);
![[Maple Plot]](images/FPSSols61.gif)
> NewtonRaphson(f,0.0,.0001,100);
![]()
> NewtonRaphson(f,2.0,.0001,100);
![]()
> NewtonRaphson(f,4.0,.0001,100);
![]()
> NewtonRaphson(f,8.0,.0001,100);
![]()
E)
> x2[1]:=.585786: x2[2]:=3.414214: c2[1]:=.853553: c2[2]:=.146447:
> x3[1]:=.415775: x3[2]:=2.294280: x3[3]:=6.289945: c3[1]:=.711093: c3[2]:=.278518: c3[3]:=.010389:
> x4[1]:=.322548: x4[2]:=1.745761: x4[3]:=4.536620: x4[4]:=9.395071: c4[1]:=.603154:
> c4[2]:=.357419: c4[3]:=.038888: c4[4]:=.000539:
> f:=x->x^5-2*x^3;
![]()
> add(evalf(c2[i]*f(x2[i])),i=1..2);
![]()
> add(evalf(c3[i]*f(x3[i])),i=1..3);
![]()
> add(evalf(c4[i]*f(x4[i])),i=1..4);
![]()
The exact value is 108. The reason is that
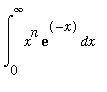 =
n
! for all
n
>= 0, so
=
n
! for all
n
>= 0, so
this integral gives 5! - 2*3! = 108. Here is a proof of the formula
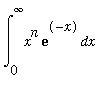 =
n
!
=
n
!
by induction on
n.
The base case is
n =
0:
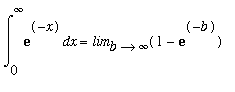 = 1 = 0!
= 1 = 0!
The induction step uses integration by parts:
u =
![]() and
and

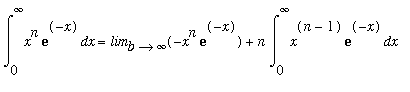
= 0 +
![]() =
n
!
=
n
!
by the induction hypothesis.
IV.
> f:=(t,y)->-20*y;
![]()
> T[0] := 0: RKW[0]:=1:
> h:=.2:
> for i to 15 do
> k[1]:=f(T[i-1],RKW[i-1])*h;
> k[2]:=f(T[i-1]+h/2,RKW[i-1]+k[1]/2)*h;
> k[3]:=f(T[i-1]+h/2,RKW[i-1]+k[2]/2)*h;
> k[4]:=f(T[i-1]+h,RKW[i-1]+k[3])*h;
> RKW[i]:=RKW[i-1]+(k[1]+2*k[2]+2*k[3]+k[4])/6;
> T[i]:=T[i-1]+h;
> end do:
> for i from 0 to 15 do
> lprint("exact:",exp(-20*T[i]),"Runge-Kutta:",RKW[i]);
> end do:
"exact:", 1, "Runge-Kutta:", 1
"exact:", .1831563889e-1, "Runge-Kutta:", 4.999999999
"exact:", .3354626279e-3, "Runge-Kutta:", 25.00000000
"exact:", .6144212353e-5, "Runge-Kutta:", 125.0000000
"exact:", .1125351747e-6, "Runge-Kutta:", 625.0000001
"exact:", .2061153622e-8, "Runge-Kutta:", 3125.000000
"exact:", .3775134544e-10, "Runge-Kutta:", 15625.00000
"exact:", .6914400107e-12, "Runge-Kutta:", 78124.99996
"exact:", .1266416555e-13, "Runge-Kutta:", 390624.9997
"exact:", .2319522830e-15, "Runge-Kutta:", 1953124.997
"exact:", .4248354255e-17, "Runge-Kutta:", 9765624.982
"exact:", .7781132241e-19, "Runge-Kutta:", 48828124.91
"exact:", .1425164083e-20, "Runge-Kutta:", 244140624.6
"exact:", .2610279070e-22, "Runge-Kutta:", 1220703122.
"exact:", .4780892884e-24, "Runge-Kutta:", 6103515611.
"exact:", .8756510763e-26, "Runge-Kutta:", .3051757805e11
Notice that the exact solution values are tending rapidly to zero, while
the Runge-Kutta approximations seem to be growing without bound(!)
B)
![]() = 5 > 1 if
h =
.2 and
= 5 > 1 if
h =
.2 and
![]() , but with
h = .
1, we get
, but with
h = .
1, we get
something < 1. This explains why the results in part A were so bad.
We are essentially multiplying
![]() by 5 in each Runge Kutta step(!)
by 5 in each Runge Kutta step(!)
> h:='h';
![]()
> plot(sum((-20*h)^j/j!,j=0..4),h=0..0.2);
![[Maple Plot]](images/FPSSols82.gif)
To get
![]() < 1, we need
h <
.14 or so. Running Runge-Kutta again
< 1, we need
h <
.14 or so. Running Runge-Kutta again
gives approximate values tending to zero, but the approximation to the actual
solution is still not very good.
This is an example of what is called a "stiff" differential equation. Special
techniques are needed to get accurate approximations to solutions of these!