MATH 241 -- Multivariable Calculus
Differentiability for 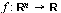
September 21, 2007
We consider the function 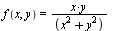 for
for 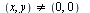 (and
(and 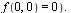
This function has partial derivatives 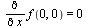 and
and 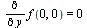
| > |
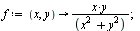 |
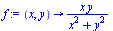 |
(1) |
| > |
The graph together with its ``tangent plane'' 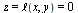 |
| > |
![plot3d([0, f(x, y)], x = -3 .. 3, y = -3 .. 3, grid = [60, 60]); 1](images/Diff_10.gif) |
The tangent plane does not seem to have anything to do with the shape of the graph
in this example. Indeed, it it is not even the case that 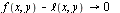 as
as
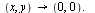 Next, consider the function
Next, consider the function 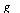 given by:
given by:
| > |
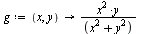 |
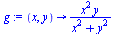 |
(2) |
| > |
![plot3d(g(x, y), x = -3 .. 3, y = -3 .. 3, grid = [60, 60]); 1](images/Diff_17.gif) |
Here again, 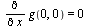 and
and 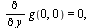 and unlike the first example
and unlike the first example 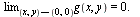 But from
But from
| > |
![plot3d(`/`(`*`(`+`(g(x, y), 0)), `*`(sqrt(`+`(`*`(`^`(x, 2)), `*`(`^`(y, 2)))))), x = -3 .. 3, y = -3 .. 3, grid = [50, 50]); 1](images/Diff_22.gif) |
we suspect that the approximation is not ``especially good.''
Let's see what is true about the partial derivative functions for 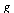
| > |
)](images/Diff_25.gif) |
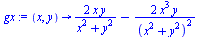 |
(3) |
| > |
)](images/Diff_27.gif) |
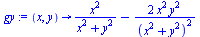 |
(4) |
| > |
![plot3d(gx(x, y), x = -3 .. 3, y = -3 .. 3, grid = [50, 50]); 1](images/Diff_29.gif) |
From this, we can see that 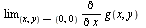 does not exist, so
does not exist, so 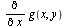 is not
is not
continuous at (0,0).
![]()
![]() for
for ![]() (and
(and ![]()
![]() and
and ![]()

![]() as
as ![]() Next, consider the function
Next, consider the function ![]() given by:
given by: 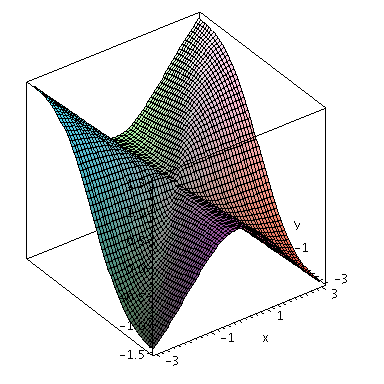
![]() and
and ![]() and unlike the first example
and unlike the first example ![]() But from
But from 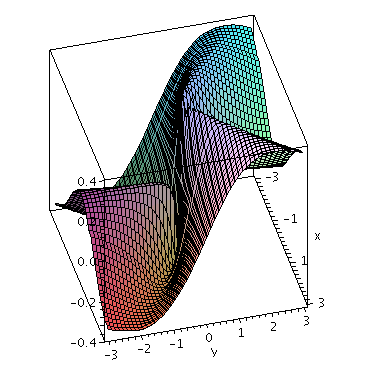
![]()
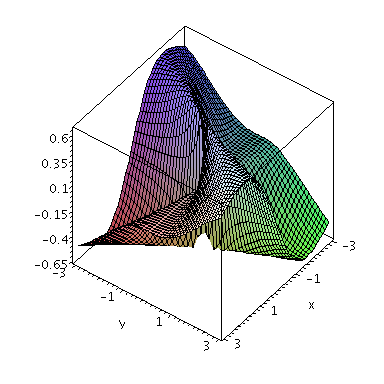
![]() does not exist, so
does not exist, so ![]() is not
is not