MONT 109N -- Bhaskara's Approximation of the sine
April 11, 2011

In the text known as the Maha Bhaskariya (c. 600 CE), the classical-period
Indian mathematician Bhaskara developed the following approximation to
the sine function (given for an angle in degrees, with the radius of the
circle set to   

(1)

 

Here are Bhaskara's approximation for the sine of 23 degrees,
and a more accurate approximation using a different modern
method: 

 

	(2)

 

Note that the Bhaskara formula gives the value correct to 2 decimal places

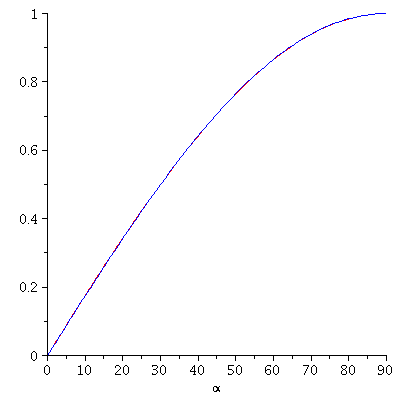
In fact if we plot both formulas on the interval from 0 to 90 degrees, it is difficult  

to tell that we are looking at two different functions -- the agreement is close
enough that hardly any difference is apparent at the resolution of the graphics: