MATH 132 -- Lab Day 2

Solutions

March 22, 2005

A)  The catenary-shaped cables

>	fcat:=x->(exp(a*x)+exp(-a*x))/2 - 1;

>	eq:=fcat(640)=143;

>	subs(a=2,fcat(x));

>	aval:=fsolve(eq,a=1);

>	plot(subs(a=aval,fcat(x)),x=-640..640);

>	fcats:=subs(a=aval,fcat);

>	evalf(Int(sqrt(1+diff(fcats,x)^2),x=-640..640));

B)  Parabolic cables.  First, we find a value for   k    in the parabolic form   y = k

     to make   y = 143 (meters above low point), when x = 640:  

>	kcold:=evalf(143/(640)^2);

>	plot(kcold*x^2,x=-640..640);

C)  The parabolic cable length

>	cold:=evalf(Int(sqrt(1+diff(kcold*x^2,x)^2),x=-640..640));

D) Check using the Pythagorean theorem:

>	evalf(2*sqrt(640^2+143^2));

This is reasonable, since we expect the length of the curved parabolic cables to

be close to, but slightly larger than, the length of the straight line segments.

E)  The ``hot'' cables.  The rationale for the following computations is this:  When hot,

      the cables will still be parabolic in shape.  So we again take the equation   y = k

      but with a different   k   from before.   Note:  this means we are shifting the

       cables up from their actual position, to place the low point at  y = 0 again.

      We know the length of the hot cables is  1.0005 times the cold length, so

      we set up the equation:

>	eqn:=int(sqrt(1+diff(k*x^2,x)^2),x=-640..640) = 1.0005*cold;

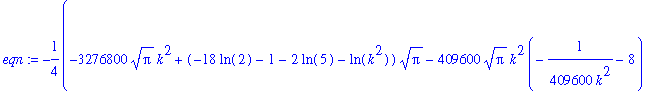
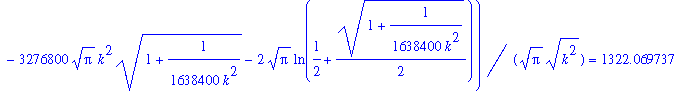
and solve it to find the value of   k   for the hot cables:

>	khot:=fsolve(eqn,k=kcold);

>	hot:=evalf(Int(sqrt(1+diff(khot*x^2,x)^2),x=-640..640));

(This checks that we get the correct arc length.)  Now, the ``sag'' for the hot

cables is the vertical distance between the point at the top  (with   x = 640 )  and

the bottom   (x = y = 0):

>	newsag:=khot*640^2;

This is just over 1 meter larger than the sag when the cables are cold (143 m).  This is probably

not noticeable for cars traveling over the bridge.