| > |
| > |
MATH 244 -- Linear Algebra Section 1
Problem Set 9 Solutions
April 20, 2007
Section 5.2
6. The characteristic polynomial is 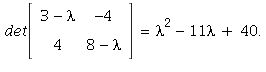
The eigenvalues are the roots of 0 = ![]() so by the quadratic
so by the quadratic
formula:
![]()
![]()
![]()
Neither root is real, so there are no real eigenvalues.
10. The characteristic polynomial is
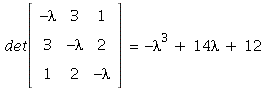 (after expanding out and simplifying).
(after expanding out and simplifying).
14. The characteristic polynomial is (expanding determinant along row 2):
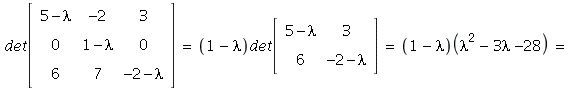
![]()
18. The eigenspace for ![]() is:
is:
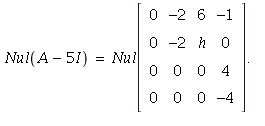 If we consider reducing this to row-reduced
If we consider reducing this to row-reduced
echelon form, then there is only one free variable in the system ![]()
unless ![]() For h = 6, we have rref =
For h = 6, we have rref = 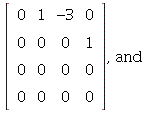
![]()
, Vector[column](%id = 138526992)})](images/PS9Sol_16.gif) dimension 2. In all other cases
dimension 2. In all other cases ![]()
23. If ![]() then
then 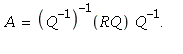 This shows that
This shows that ![]() and
and
![]() are similar since the invertible matrix
are similar since the invertible matrix ![]() satisfies
satisfies ![]()
(see the definition at bottom of page 314 in the text).
25. a) By direct calculation, ) = Vector[column](%id = 136084140) and Vector[column](%id = 136084140) = Vector[column](%id = 140169988)](images/PS9Sol_24.gif)
so the given vector is an eigenvector with eigenvalue λ = 1. The characteristic
polynomial is ![]() so the other eigenvalue is
so the other eigenvalue is
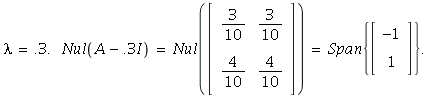 Since the eigenvalues
Since the eigenvalues
1 and .3 are distinct, the set , Vector[column](%id = 135143236)}](images/PS9Sol_27.gif) is linearly independent (Theorem 2 on
is linearly independent (Theorem 2 on
page 307 of the text, or direct check), hence a basis for ![]()
b) ![]()
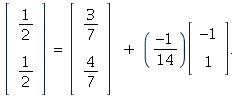
c) This is similar to the computations you did on Discussion 3:
![x[1] = Ax[0] and Ax[0] = (Matrix(%id = 140198924))(Vector[column](%id = 139342576)+`.`(-1/14, Vector[column](%id = 138411204))) and (Matrix(%id = 140198924))(Vector[column](%id = 139342576)+`.`(-1/14,...](images/PS9Sol_31.gif)
![]()
![x[2] = Ax[1] and Ax[1] = (Matrix(%id = 136393492))(Vector[column](%id = 136328928)+`.`((-1/14)(.3), Vector[column](%id = 135967588))) and (Matrix(%id = 136393492))(Vector[column](%id = 136328928)+`.`(...](images/PS9Sol_33.gif)
![x[2] = Ax[1] and Ax[1] = (Matrix(%id = 136393492))(Vector[column](%id = 136328928)+`.`((-1/14)(.3), Vector[column](%id = 135967588))) and (Matrix(%id = 136393492))(Vector[column](%id = 136328928)+`.`(...](images/PS9Sol_34.gif)
Similarly, for all ![]() , by mathematical induction,
, by mathematical induction,
![]()
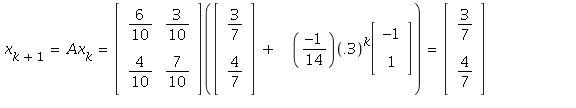

In the limit as 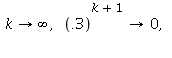 so
so 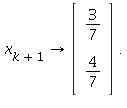
Section 5.3
12. Given that the eigenvalues are ![]() we have
we have
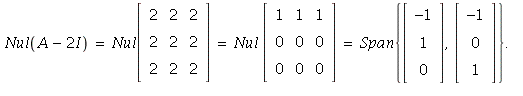
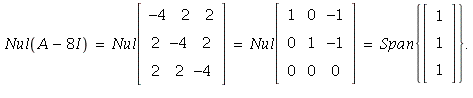
Then, ℬ = , Vector[column](%id = 138003488), Vector[column](%id = 140090712)}](images/PS9Sol_44.gif) is a basis for
is a basis for ![]() consisting of eigenvectors
consisting of eigenvectors
of A. This shows that A is diagonalizable, with 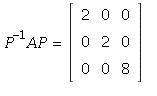 for
for
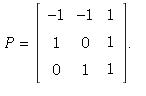 Check:
Check:
| > |
![table( [( 3, 3 ) = 8, ( 2, 2 ) = 2, ( 3, 2 ) = 0, ( 2, 1 ) = 0, ( 3, 1 ) = 0, ( 2, 3 ) = 0, ( 1, 2 ) = 0, ( 1, 3 ) = 0, ( 1, 1 ) = 2 ] )](images/PS9Sol_51.gif)
14. Given the eigenvalues are ![]() (characteristic polynomial factors as
(characteristic polynomial factors as
![]() Theorem 7 on page 326 implies that in order for
Theorem 7 on page 326 implies that in order for
A to be diagonalizable, we must have ![]()
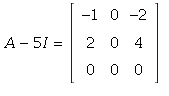 which is row-equivalent to
which is row-equivalent to 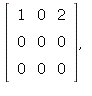 so there are 2 free
so there are 2 free
variables in the homogeneous system ![]()
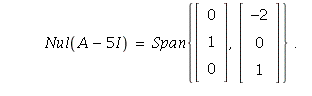 Then
Then 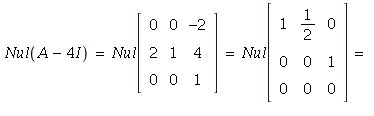
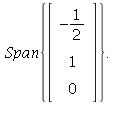 This shows that A is diagonalizable with
This shows that A is diagonalizable with 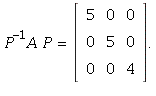
| > |
![table( [( 3, 3 ) = 0, ( 2, 2 ) = 0, ( 3, 2 ) = 1, ( 2, 1 ) = 1, ( 3, 1 ) = 0, ( 2, 3 ) = 1, ( 1, 2 ) = -2, ( 1, 3 ) = -1/2, ( 1, 1 ) = 0 ] )](images/PS9Sol_63.gif)
| > |
![table( [( 3, 3 ) = 5, ( 2, 2 ) = 5, ( 3, 2 ) = 0, ( 2, 1 ) = 2, ( 3, 1 ) = 0, ( 2, 3 ) = 4, ( 1, 2 ) = 0, ( 1, 3 ) = -2, ( 1, 1 ) = 4 ] )](images/PS9Sol_65.gif)
| > |
![table( [( 3, 3 ) = 4, ( 2, 2 ) = 5, ( 3, 2 ) = 0, ( 2, 1 ) = 0, ( 3, 1 ) = 0, ( 2, 3 ) = 0, ( 1, 2 ) = 0, ( 1, 3 ) = 0, ( 1, 1 ) = 5 ] )](images/PS9Sol_67.gif)
24. No -- the hypotheses of Theorem 7 on page 324 cannot be satisfied in
this case. The largest linearly independent set of eigenvectors will have
size 2, so there is no basis consisting of ![]() consisting of eigenvectors of A.
consisting of eigenvectors of A.
26. Yes -- if the remaining eigenspace has dimension only 1, then the matrix
is not diagonalizable (see Theorem7). The following matrix gives an example
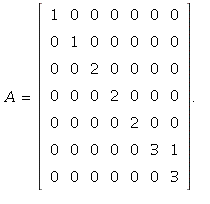 The eigenvalues are
The eigenvalues are ![]() (with multiplicity 2),
(with multiplicity 2),
![]() with multiplicity 3) , and
with multiplicity 3) , and ![]() (with multiplicity 2). By the form of the
(with multiplicity 2). By the form of the
matrix ![]() has dimension 2,
has dimension 2, ![]()
has dimension 3, but ![]()
32. Since A is not invertible, ![]() must be one of the eigenvalues (see Theorem on page
must be one of the eigenvalues (see Theorem on page
312 -- continuation of the Invertible Matrix Theorem). By Theorem 6 on page 323,
if the other eigenvalue is ![]() (or anything other than 0), then A will be diagonalizable.
(or anything other than 0), then A will be diagonalizable.
This means that A should be similar to the diagonal matrix 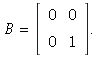 To get
To get
![]() not diagonal we can try taking an arbitrary invertible matrix like
not diagonal we can try taking an arbitrary invertible matrix like 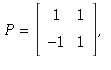 with
with
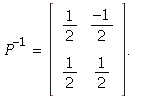 Then
Then ![]()
| > |
![table( [( 2, 2 ) = 1/2, ( 2, 1 ) = -1/2, ( 1, 2 ) = -1/2, ( 1, 1 ) = 1/2 ] )](images/PS9Sol_85.gif)
is a matrix that satisfies all of the properties we want.
Section 6.2
6. Call the three vectors ![]() We have
We have
![]()
![]()
![]()
So the set is not orthogonal. (It would be enough just to show ![]()
of course).
10. It is clear that ![]() here. This implies that
here. This implies that
![]() is an orthogonal set. By Theorem 4 in this section, it
is an orthogonal set. By Theorem 4 in this section, it
follows that ![]() is linearly independent. (This can also be checked
is linearly independent. (This can also be checked
directly: If ![]() for some scalars
for some scalars ![]() then
then
we can take dot products with ![]()
0 = ![]()
Since ![]() Similarly, dotting with
Similarly, dotting with ![]() shows
shows ![]() and
and
dotting with ![]() shows
shows ![]() It follows that
It follows that![]() is a basis for
is a basis for ![]()
Then because of the orthogonality, there is a shortcut we can use for
computing the weights in a linear combination:
![]()
For each i, i = 1, 2, 3, we have
![]() (since the dot product of
(since the dot product of ![]() with the other two terms
with the other two terms
is zero).
Hence ![c[i] = x*u[i]/`*`(u[i], u[i])](images/PS9Sol_108.gif) for each i = 1, 2, 3.
for each i = 1, 2, 3.
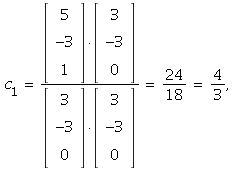
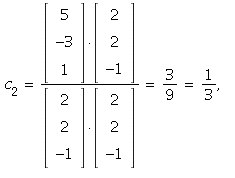
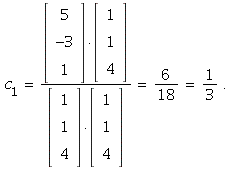
12. The orthogonal projection on the line spanned by ](images/PS9Sol_112.gif) is defined by
is defined by
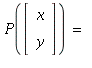
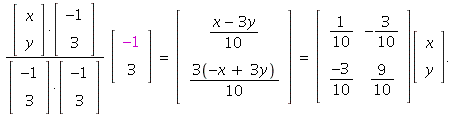
With 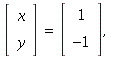 we get
we get 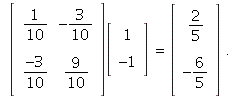
| > |
![]()
| > |
![table( [( 3, 3 ) = 8, ( 2, 2 ) = 2, ( 3, 2 ) = 0, ( 2, 1 ) = 0, ( 3, 1 ) = 0, ( 2, 3 ) = 0, ( 1, 2 ) = 0, ( 1, 3 ) = 0, ( 1, 1 ) = 2 ] )](images/PS9Sol_122.gif)
| > |