>

 

>

 

MATH 244 -- Linear Algebra 

Problem Set 8 Solutions 

April 13, 2007 

Section 4.7 

4.   is the change of coordinates matrix from    to  , so 

     equation (i) is the correct one. 

6.   a) 

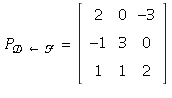
           (the i th column is the coordinate vector ) 

     b)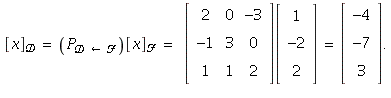   

8.   One way to do questions like this is to relate both bases 

     to the standard basis in  Write   

      = Then 

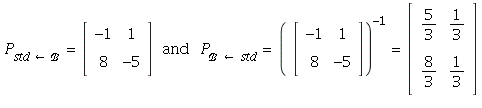
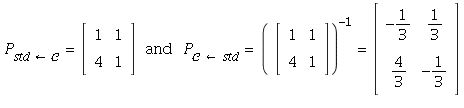
      Therefore,   

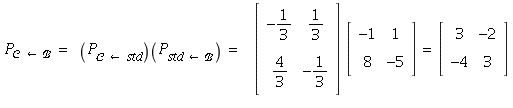
      and  

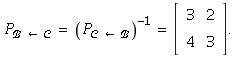
14.  The standard basis here is the basis for  We have 

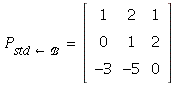      and   

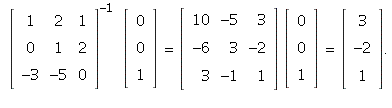
       Check:   

Section 5.4 

2.  By the definition, 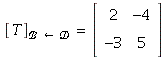    (the columns are 

    the coordinate vectors of with respect to ℬ. 

4.   By the definition,  

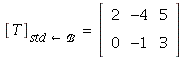
     (For instance,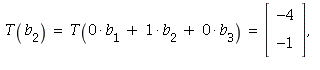  

     which gives the second column of the matrix.  The other columns 

     are similar.) 

6.   a)   

     b)  We have   

          for all  Similarly, for all and all  

          Therefore, 

          is a linear transformation. 

     c)  By the definition, 

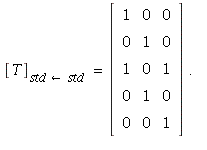          (For instance, the last column is  

          the coordinate vector of   

    d)  (added part).  Let ℬ =  

         We want   

         =

 

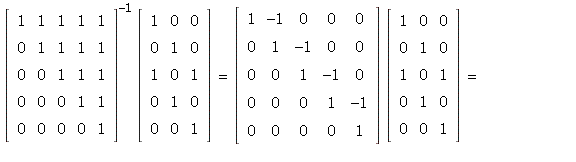
8.   If   then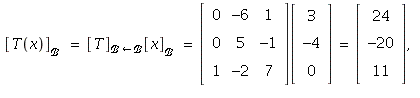   

     so  

10.  a)   

           = Similarly,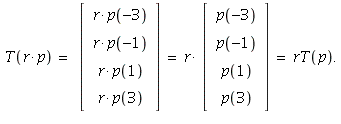   

            Therefore,  T  is a linear mapping. 

     b)    By the definition, 

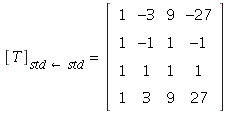
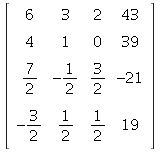
    c)  (added part)   

                          =  

                          =  

                          =  

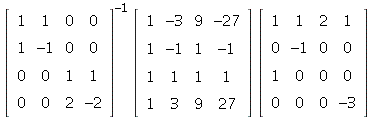
Section 5.1 

2.  If 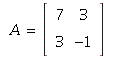then 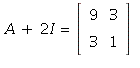 has rank 1. 

    There are nonzero vectors such as  such that  

     Therefore  is an  

     eigenvalue of   

6.   We have 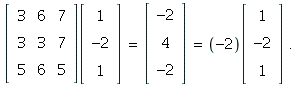 Therefore, 

     this is an eigenvector of the given matrix with eigenvalue  

8. 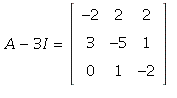  has determinant  

    (expanding by cofactors along row 3).  Hence it has  

    rank ≤ 2, and there are nonzero vectors x  such that  

    One such vector is (found from 

    the row-reduced echelon form of  which is  

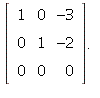
20.  Since the dimension of the column space is 1,  

      the matrix is not invertible.  This means that  

      so λ = 0 is an eigenvalue.   

      Span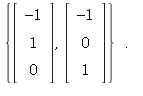These are two linearly independent 

      eigenvectors for the eigenvalue λ = 0.  (Note:  λ = 15 is   

      also an eigenvalue.) 

24.  The matrix 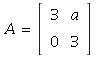is one such matrix for any real value of  a. 

        so is the only eigenvalue. 

25.  If λ is an eigenvalue of the invertible matrix A,  then there 

     is a nonzero vector  x  such that  Note that  

     since otherwise we would have a nonzero vector in   

     which is a contradiction to the Invertible Matrix Theorem.  But 

     then from  we can multiply both sides by  to  

     yield   Then divide through by  λ  to  

     obtain  This equation shows that is an eigenvalue 

     of  

26.  If  and   is an eigenvector (nonzero) with eigenvalue 

     then  implies  

     But  is the zero matrix so (the zero vector), so  

     Hence λ = 0.   

36.  The figure should show (the vector in the same direction 

      as  v  but 3 times as long),  (the vector in the opposite 

      direction along the line spanned by  and  

      found by the parallelogram law for vector addition.   

>

 

>

 

>

 

>