| > |
| > |
MATH 244 -- Linear Algebra
Problem Set 7 Solutions
March 30, 2007
Section 4.3
24. Let A be the n x n matrix with columns ![]()
By the Invertible Matrix Theorem (section 2.3)
A is invertible. Hence for all ![]() the
the
system of linear equations ![]() has a solution.
has a solution.
But this implies Span(ℬ) ![]() Therefore, ℬ
Therefore, ℬ
is a basis for ![]()
(Note: this also follows from the reasoning given
in the proof of Section 4.5/26 below.)
26. The set S = ![]() is linearly
is linearly
dependent because of a trigonometric identity:
![]() for all t. Hence
for all t. Hence ![]()
The set ![]() is linearly independent
is linearly independent
since if ![]() for all t, then
for all t, then
setting 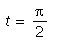 shows
shows ![]() hence
hence ![]()
But then ![]() as well, since
as well, since ![]() is not the zero
is not the zero
function.
31. If ![]() is linearly dependent, then there exist
is linearly dependent, then there exist
scalars ![]() not all equal to zero such that 0 =
not all equal to zero such that 0 = ![]()
Since T is assumed to be a linear mapping, applying it
to both sides of the last equation shows
![]()
![]()
But ![]() for all linear mappings so
for all linear mappings so
0 = ![]()
Since the ![]() are not all zero (they are the same scalars as
are not all zero (they are the same scalars as
in the original linear dependence on the ![]() this shows that
this shows that
![]() is also linearly dependent.
is also linearly dependent.
32. Assume that there are scalars ![]() not all equal to zero such that
not all equal to zero such that
![]() =
= ![]() Since
Since ![]() is linear, this implies
is linear, this implies
![]() Since T is one-to-one,
Since T is one-to-one,
this implies that ![]() =
= ![]() Since
Since ![]() are not all
are not all
equal to zero, this implies that ![]() is linearly dependent.
is linearly dependent.
34. ``By inspection'', ![]() As in 24 above, this
As in 24 above, this
relation shows ![]() or the span of
or the span of
any of the other two-element subsets). The set ![]() is linearly
is linearly
independent since ![]() as a polynomial
as a polynomial
implies ![]() It is easy to check that
It is easy to check that
the only solution of this 2 x 2 homogeneous system of linear
equations is ![]() Thus,
Thus, ![]() is one basis for
is one basis for
![]()
Section 4.4
10. By the standard ``recipe''
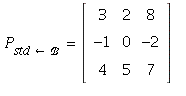
(The columns of this matrix are the coordinate vectors of the
basis ℬ with respect to the standard basis.)
12. 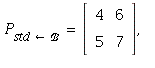 so
so 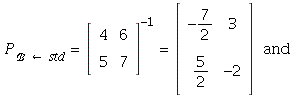
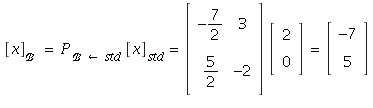
14. We can follow the method used in problem 12. Take
the "standard basis" ![]() Then
Then
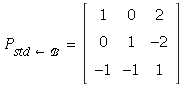 (columns are the coordinate vectors of the
(columns are the coordinate vectors of the
polynomials in ℬ).
| > |
![table( [( 2, 3 ) = 2, ( 1, 1 ) = -1, ( 3, 3 ) = 1, ( 1, 2 ) = -2, ( 2, 1 ) = 2, ( 3, 2 ) = 1, ( 2, 2 ) = 3, ( 1, 3 ) = -2, ( 3, 1 ) = 1 ] )](images/PS7Sol_51.gif)
Then
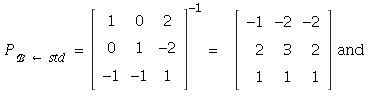
![[p][`ℬ`] = `.`(Matrix(%id = 138498076), Vector[column](%id = 140002428)) and `.`(Matrix(%id = 138498076), Vector[column](%id = 140002428)) = Vector[column](%id = 138315780)](images/PS7Sol_53.gif)
Check: ![]() OK!
OK!
18. Follow the standard ``recipe'' for getting the coordinate
vectors. The unique linear combination of the vectors in ℬ
that equals ![]() is
is
![]()
Picking off the scalars here and placing them into a vector
in ![]() we get
we get ![]() the ith standard basis vector, which is the
the ith standard basis vector, which is the
same as the ith column of the n x n identity matrix.
22. The matrix that does this is the change of coordinates matrix
![]() This is the inverse of the matrix whose
This is the inverse of the matrix whose
columns are the (standard coordinates) of the vectors in the basis
ℬ.
28. With respect to the basis ![]() for
for ![]() the coordinate
the coordinate
vectors of the polynomials are
, Vector[column](%id = 136751716), Vector[column](%id = 139927240)](images/PS7Sol_62.gif)
The mapping ![]() is an isomorphism of vector spaces
is an isomorphism of vector spaces
(linear, 1-1, and onto). This implies that the polynomials are
linearly independent if and only if the coordinate vectors are.
To check linear dependence or independence, we apply our
standard methods. Reducing the 4 x 3 matrix with these
columns to echelon form we find:
| > |
![table( [( 2, 3 ) = 3, ( 1, 1 ) = 1, ( 3, 3 ) = 0, ( 1, 2 ) = 0, ( 2, 1 ) = 0, ( 3, 2 ) = 0, ( 4, 3 ) = 0, ( 4, 1 ) = 0, ( 2, 2 ) = 1, ( 1, 3 ) = 1, ( 4, 2 ) = 0, ( 3, 1 ) = 0 ] )](images/PS7Sol_65.gif)
Since there is a free variable in the corresponding homogeneous
system, there is a nontrivial solution, so the vectors (and polynomials)
are linearly dependent.
Section 4.5
26. Let ℬ = ![]() be a basis for H.
be a basis for H.
We will argue by contradiction. Suppose
H is strictly contained in V. Then there is some ![]()
such that ![]() We claim that the set =
We claim that the set = ![]()
![]() must be linearly independent.
must be linearly independent.
To see this, consider a linear combination
![]()
If ![]() then we could use this equation to solve for
then we could use this equation to solve for
x, and that would say ![]() So
So ![]()
But then the remaining terms only involve vectors in
ℬ and we are assuming ℬ is a basis, hence linearly
independent. Therefore ![]() for all i. But this
for all i. But this
leads to a contradiction because ![]() also.
also.
In an ![]() dimensional vector space, any set of
dimensional vector space, any set of ![]()
vectors is linearly dependent (Theorem 9 in this section
of the text). Therefore ![]()
28. The subset ![]() for all
for all ![]()
spans the subspace of ![]() consisting of all polynomial
consisting of all polynomial
functions. This set is linearly independent because
any nonzero polynomial has only finitely many real roots.
(That is, the only polynomial that is the zero function
is the zero polynomial, with all coefficients equal to zero.)
This implies that ![]() is not a finite-dimensional vector
is not a finite-dimensional vector
space (Theorem 9 again -- in a vector space of dimension
n, the largest linearly independent sets have n elements).
32. To prove ![]() it suffices to show that if
it suffices to show that if
![]() is a basis for
is a basis for ![]() then
then ![]()
is a basis for ![]() do you see why?)
do you see why?)
First, note that the results of problems 31 and 32 from section
4.3 above say that when T is 1-1 (as assumed here),
![]() is linearly dependent if and only if
is linearly dependent if and only if
![]() is linearly dependent. Thus, it follows by logic that
is linearly dependent. Thus, it follows by logic that
![]() is linearly independent if and only if
is linearly independent if and only if
![]() is linearly independent too.
is linearly independent too.
Next, since ![]() for all
for all ![]() we have
we have
![]()
for some scalars ![]() Since T is linear this implies
Since T is linear this implies
![]()
![]()
This shows ![]() is contained in
is contained in
![]() On the other hand, we can
On the other hand, we can
take any linear combination as on the right of the last equation,
use the linearity of T ``in reverse'', and see that it equals
![]() for some
for some ![]() This shows that
This shows that ![]()
is equal to ![]() Since
Since ![]() spans
spans ![]() and
and
is linearly independent, it is a basis for ![]()