| > |
MATH 244 -- Linear Algebra
Problem Set 6 Solutions
March 16, 2007
Section 3.3
4. By Cramer's Rule, the solution is
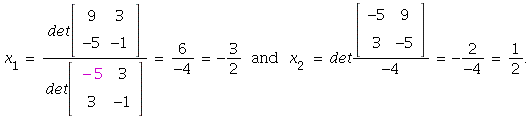
6. By Cramer's Rule,
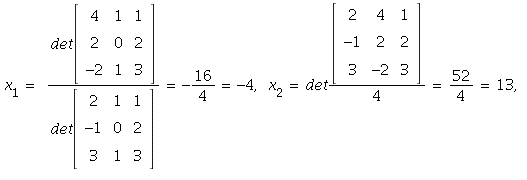
![x[3] = 1/4*det*Matrix(%id = 136042832) and 1/4*det*Matrix(%id = 136042832) = -`*`(4, 1/4) and -`*`(4, 1/4) = -1.](images/PS6Sol_4.gif)
8. There is a unique solution when 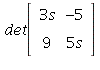
![]()
This is true for all real s. By Cramer's Rule, the solution is
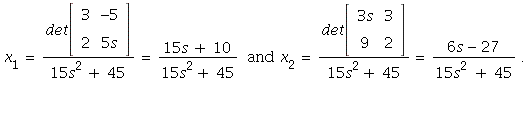
20. The area of the parallelogram is
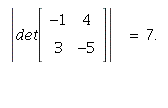
24. The volume is
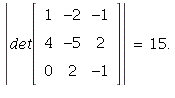
29. Since the diagonal ![]() of the parallelogram with
of the parallelogram with
vertices ![]() and
and ![]()
divides the parallelogram into two congruent triangles,
the area of the triangle is one half of the area of the
parallelogram:
![]()
where ![]() is the
is the ![]() matrix with columns
matrix with columns ![]()
30. If we translate the triangle to place ![]() at the origin,
at the origin,
the other vertices are ![]()
![]() Applying the formula from problem
Applying the formula from problem
29, the area is
![]()
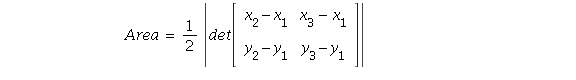
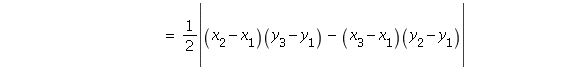
Now on the other hand, if we consider the ![]() matrix given
matrix given
in the problem, we can apply row operations to evaluate
the determinant as follows -- replace row 2 by row 2 - row 1
and replace row 3 by row 3 - row 1:
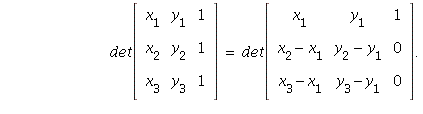
Expanding the determinant along the third column gives
= ![]()
which is the same as the result above, which shows the equality
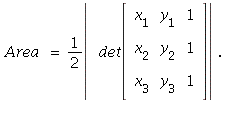
32. a) There are several such mappings, but the "obvious" one
is the ![]() defined by the
defined by the ![]() matrix A
matrix A
whose columns are the vectors ![]() (in that order).
(in that order).
Then ![]() for each
for each ![]()
b) By Theorem 10, ![]() where
where ![]() is the matrix
is the matrix
described in part a.
Section 4.1
2. a) Yes: If ![]() then
then ![]() So the vector
So the vector ![]()
satisfies ![]() Hence
Hence ![]()
b) If ![]() then
then ![]()
4. The figure should show a line L not passing through (0,0),
two vectors ![]() from the origin to points on L, and their
from the origin to points on L, and their
vector sum ![]() constructed by the parallelogram law
constructed by the parallelogram law
for vector addition in ![]() The head of the vector sum is
The head of the vector sum is
not on the line L, so L is not closed under vector sums.
5. The set W of all polynomials![]() is a vector subspace of
is a vector subspace of
![]() because: (a) If we take
because: (a) If we take ![]()
(b) If ![]() then
then ![]()
(c) If ![]() and
and ![]() then
then ![]()
6. The set ![]() of polynomials
of polynomials ![]() is not a vector
is not a vector
subspace of ![]() because 0
because 0 ![]() W. (The other two properties
W. (The other two properties
also fail, but one is sufficient to say W is not a subspace.)
8. The set ![]() of polynomials
of polynomials ![]() such that
such that ![]()
is a vector subspace of ![]() for each
for each ![]() . (a) The
. (a) The
zero polynomial ![]() satisfies
satisfies ![]()
(b) If ![]() then
then ![]()
(c) If ![]() then
then ![]()
20. a) We need to know that the zero function is continuous,
that sums of continuous functions are continuous, and
that a constant times a continuous function is continuous.
b) Let ![]() The zero function z is in
The zero function z is in
![]() because
because ![]() If
If ![]() then
then
![]()
so ![]() Finally, if
Finally, if![]() then
then
![]() so
so ![]()
21. ![]() is a vector subspace of the vector space
is a vector subspace of the vector space ![]() because
because
(a) the zero matrix is in H (take ![]() in the general
in the general
form).
(b) If ![]() then
then 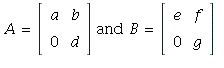 for some
for some
![]() Hence
Hence 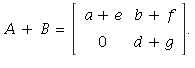
This matrix is in H (because of the zero in the second row,
first column).
(c) If 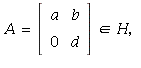 and
and ![]() then
then 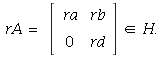
22. H is a vector subspace of ![]() because
because
(a) ![]() so
so ![]()
(b) If ![]() then
then ![]()
This shows ![]()
(c) If ![]() then
then ![]()
Hence ![]()
31. If ![]() is a subspace and
is a subspace and ![]() then by property c in
then by property c in
the definition of a subspace, for all scalars ![]()
![]() Then, by property b in the definition,
Then, by property b in the definition,
![]() The set
The set ![]() consists of all the
consists of all the
linear combinations ![]() so we have shown
so we have shown ![]()
32. If ![]() are subspaces, they satisfy all three properties in
are subspaces, they satisfy all three properties in
the definition. Hence ![]() Therefore,
Therefore, ![]()
If ![]() then
then ![]() Therefore,
Therefore,
![]() But this says
But this says ![]()
Finally, if ![]() then
then ![]() so
so ![]()
Similarly, ![]() so
so ![]() This implies
This implies ![]()
Since ![]() satisfies the three properties for a subspace
satisfies the three properties for a subspace
it is itself a subspace.
For the last part, consider ![]()
and ![]() These are vector subspaces
These are vector subspaces
of ![]() The union
The union ![]() is not a vector subspace, though,
is not a vector subspace, though,
because, for instance, ![]() but
but ![]()
33.
a. Since ![]() are assumed to be subspaces themselves,
are assumed to be subspaces themselves,
![]() and
and ![]() Hence
Hence ![]()
Next, let ![]() Then by definition,
Then by definition,
![]() and
and ![]() where
where ![]()
But then ![]() commutativity
commutativity
and associativity of vector addition). Since ![]() are subspaces,
are subspaces,
![]() and
and ![]() This shows
This shows ![]()
Finally if ![]() then
then ![]()
![]() Since
Since ![]() are subspaces,
are subspaces, ![]()
This shows ![]()
b. This is immediate since ![]() and they satisfy
and they satisfy
the three parts of the definition of subspaces.
34. Since ![]() given
given
any ![]() we have
we have ![]() for
for
some scalars ![]() Similarly,
Similarly, ![]() for some
for some
scalars ![]() But then
But then
![]()
which is in ![]() This shows
This shows
that ![]() Conversely,
Conversely,
if ![]() then for some scalars
then for some scalars
![]()
![]()
= ![]()
This shows ![]()
Because of the two inclusions, the sets are equal.
Section 4.2
30. We assume ![]() is a linear transformation and
is a linear transformation and
consider ![]() for some
for some ![]()
(a) ![]() so
so ![]() (b) Let
(b) Let ![]()
Then ![]() for some
for some ![]() Then
Then
because ![]() is linear,
is linear, ![]()
which shows ![]() (c) Finally, let
(c) Finally, let ![]()
and ![]() Then
Then ![]() for some
for some ![]() Hence
Hence
![]() This shows that
This shows that ![]()
All three properties in the definition are satisfied, so
![]() is a subspace of
is a subspace of ![]()
31. a) Let ![]() Then by the definition of T
Then by the definition of T
![]()
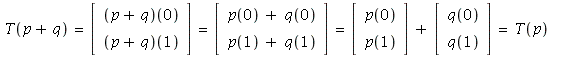
![]()
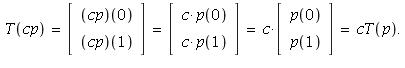
This shows T is a linear mapping.
b) The kernel of ![]() is, by definition, the set of all
is, by definition, the set of all ![]()
such that ![]() This says
This says ![]() is a quadratic
is a quadratic
polynomial with roots at ![]() Any such polynomial
Any such polynomial
is ![]() for some
for some ![]() So
So
![]()
The image (range) of ![]() is all of
is all of ![]() since for any
since for any ![]() there is
there is
a polynomial ![]() with
with ![]() and
and ![]()
fact, we can do this with a linear polynomial (the coefficient
of ![]()
33. a) If 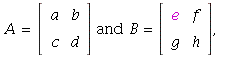 then
then
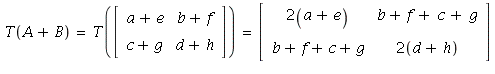
On the other hand,
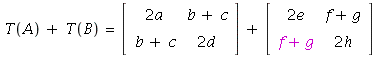
= 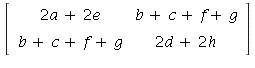
= 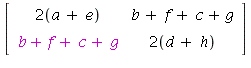
Therefore, ![]() This can
This can
also be proved by using properties of transposes.)
If 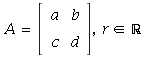 then
then
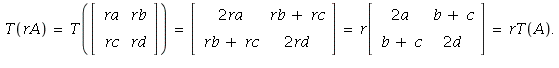
Therefore, T is linear.
b) ![]() if
if ![]() since
since ![]()
![]() since we assumed
since we assumed ![]()
c) If B is any matrix with ![]() then part b shows
then part b shows
![]() Conversely, if
Conversely, if ![]() is any matrix
is any matrix
then 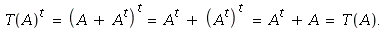
Hence the image of T equals the set of such matrices
d) ![]() the set of all matrices with
the set of all matrices with
a = 0, d = 0, b + c = 0. These can be written as
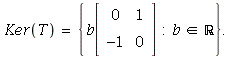
34. By the second part of the Fundamental Theorem of Calculus,
if 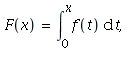 then
then ![]() Hence
Hence
our mapping can be described as 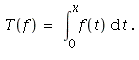
By properties of integrals,
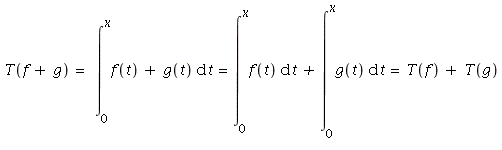
and
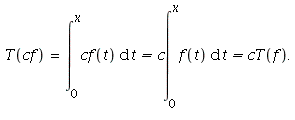
Hence T is a linear mapping.
The kernel of T is the set of all functions with ![]()
(the zero function). If we differentiate both sides of this,
we get ![]() So the only element of
So the only element of
![]() is the zero function in this case.
is the zero function in this case.
| > |