MATH 244 -- Linear Algebra
Problem Set 5 Solutions
March 2, 2007
Section 3.1
2. Along the first row:
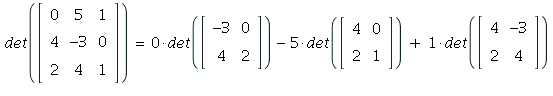
= 0 - 20 + 22 = 2
Along second column:
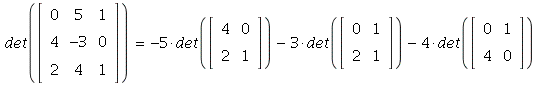
= -20 + 6 + 16 = 2.
10. The least amount of computation will be needed if we "exploit"
the zeroes in row 2, then expand the 3 x 3 minor along row 3
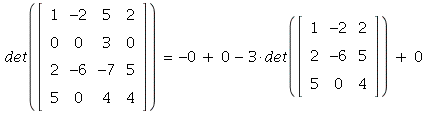
= -3(5(-10 + 12) - 0 + 4(-6 + 4))) = -3![]()
22. The row operation is ![]() This operation does not
This operation does not
change the determinant.
24. The row operation is ![]() (swap rows 1 and 2).
(swap rows 1 and 2).
This operation changes the determinant by a sign.
34. 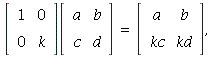 so
so ![]()
36. 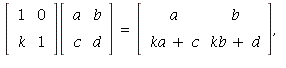 so
so ![]()
![]() since
since ![]()
38. 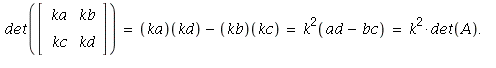
(This also follows from part c of Theorem 3 on page 192 -- one factor
of k comes from each row. See problem 32 in the next section for a generalization
of this fact. )
Section 3.2/
6. Using Theorem 3 on page 192,
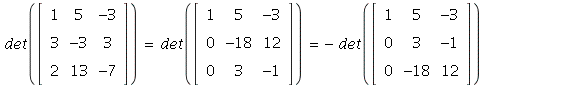
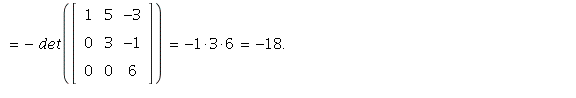
8. Doing row operations of type 1:
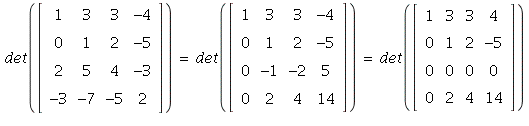
This last matrix has a whole row of zeroes, so
![]()
16. By part c of Theorem 3 on page 192, 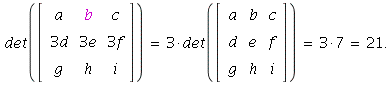
18. By part b of Theorem 3 on page 192, we can
swap rows 1 and 2, then 2 and 3:
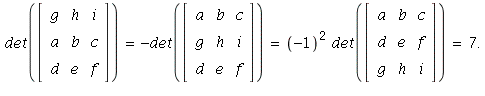
20. By part a of Theorem 3, since row 1 of the given matrix is
just row 1 plus row 2 of the known matrix,
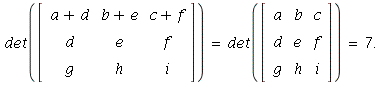
22. Expanding along row 1, for instance
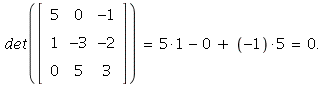 So by Theorem 4,
So by Theorem 4,
the matrix is not invertible.
31. By the product rule for determinants (Theorem 6),
![]()
We know (and this last equation also implies) ![]()
so ![]() which is what we wanted to show.
which is what we wanted to show.
32. If A is n x n, then there is a factor of r in each row
of A. Hence if we apply part c of Theorem 3 repeatedly,
![]()
(one factor of r from each row).
33. Using the product rule and the fact that ![]()
so their product commutes,
![]()
34. Using the product rule, and commutativity of multiplication
in ℝ,
![]()
However, by problem 31 above, ![]() so this simplifies
so this simplifies
to ![]() Hence
Hence ![]() which is what we wanted to
which is what we wanted to
show.
35. Note: ![]() here is the transpose of U. By Theorems 5 and 6,
here is the transpose of U. By Theorems 5 and 6,
![]()
Hence ![]() so
so ![]() is a root of
is a root of ![]() which
which
implies ![]() or
or ![]()
36. By Theorem 6,
0 = ![]()
This shows ![]() so A is not invertible by Theorem 4.
so A is not invertible by Theorem 4.
40. a. ![]() (Theorem 6)
(Theorem 6)
b. ![]() (Theorem 6)
(Theorem 6)
c. ![]() (by problem 32 above)
(by problem 32 above)
d. ![]() (Theorems 6 and 5)
(Theorems 6 and 5)
e. ![]() (as in problem 34).
(as in problem 34).
| > |
| > |