| > |
| > |
MATH 244 -- Linear Algebra, section 1
Problem Set 4 Solutions
February 23, 2007
Section 2.3
6. After replacing ![]() by
by ![]() we have
we have
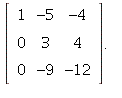 We see that rows 2 and 3 are
We see that rows 2 and 3 are
now proportional -- if we replace ![]() by
by ![]()
the last row will be all zeros. Hence A is not invertible.
8. There is a pivot in each of the 4 columns in this
upper-triangular 4 x 4 matrix, hence it is invertible.
14. A lower-triangular matrix is invertible if and only
if all of its diagonal entries are nonzero. This follows
from statement c in the Invertible Matrix Theorem (Theorem
8 in this section). In order for there to be n pivots the
diagonal entries must all be nonzero. Conversely, if all
the diagonal entries are nonzero, then there are n pivots.
15. No. By the Invertible Matrix Theorem part e,
if A is invertible, then its columns are linearly independent.
If there are two equal columns, the collection of columns
is not linearly independent, so the matrix is not invertible.
18. No. If C x = v is consistent for all v, then the mapping
defined by C is onto (part i of the Invertible Matrix Theorem).
As a result, part f also holds -- the mapping defined by C
is one-to-one, which says that C x = v has a unique solution
x for all v.
22. If the system Hx = c is inconsistent for some c,
then part i of the Invertible Matrix Theorem is not true.
The equivalence of the statements there means that
all of the other parts fail for this H. In particular,
the negation of part d holds, and there is a nontrivial
solution ![]() of the homogeneous system
of the homogeneous system ![]()
26. If the columns of A are linearly independent, then
part e of the Invertible Matrix Theorem holds, so A
is an invertible matrix (![]() exists). Since
exists). Since ![]() exists,
exists,
![]() is also an invertible matrix:
is also an invertible matrix: 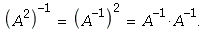
But then the Invertible Matrix Theorem implies that statement
h holds for ![]()
30. All of the statements in the Invertible Matrix Theorem
hold for A and the linear mapping defined by A.
36. Let A be the standard matrix of T. Since T
is onto, part i of the Invertible Matrix Theorem holds,
hence all the other parts hold too. In particular, A
is an invertible matrix. Since ![]() exists, we can
exists, we can
use it to define a linear transformation too, and this
is the inverse mapping ![]() is also invertible
is also invertible
(its inverse is A). So all the parts of the Invertible
Matrix Theorem also apply to ![]() and
and ![]()
In particular, ![]() is both onto and one-to-one.
is both onto and one-to-one.
(Of course, this also follows from general facts
about when inverse mappings exist and what
there properties are.)
38. The answer is No. The reason is that the given
information that ![]() for some
for some ![]() says
says
that T is not one-to-one. Hence all of the statements
in the Invertible Matrix Theorem are false for T.
In particular, T is not onto.
Section 2.8
8.
| > |
![table( [( 1, 3 ) = 0, ( 2, 4 ) = 14, ( 1, 2 ) = -2, ( 1, 1 ) = -3, ( 2, 3 ) = -6, ( 2, 1 ) = 0, ( 3, 1 ) = 6, ( 1, 4 ) = 1, ( 3, 2 ) = 3, ( 2, 2 ) = 2, ( 3, 4 ) = -9, ( 3, 3 ) = 3 ] )](images/PS4Sol_22.gif)
| > |
![table( [( 1, 3 ) = 2, ( 2, 4 ) = 7, ( 1, 2 ) = 0, ( 1, 1 ) = 1, ( 2, 3 ) = -3, ( 2, 1 ) = 0, ( 3, 1 ) = 0, ( 1, 4 ) = -5, ( 3, 2 ) = 0, ( 2, 2 ) = 1, ( 3, 4 ) = 0, ( 3, 3 ) = 0 ] )](images/PS4Sol_24.gif)
The fact that this system is consistent shows that p
is in the column space of A.
16. Not a basis for ![]() since the set is not linearly
since the set is not linearly
independent. Note that if ![]() and
and ![]() are the given
are the given
vectors, then ![]()
18.
| > |
![table( [( 1, 3 ) = 0, ( 2, 4 ) = 0, ( 1, 2 ) = 0, ( 1, 1 ) = 1, ( 2, 3 ) = 0, ( 2, 1 ) = 0, ( 3, 1 ) = 0, ( 1, 4 ) = 0, ( 3, 2 ) = 0, ( 2, 2 ) = 1, ( 3, 4 ) = 0, ( 3, 3 ) = 1 ] )](images/PS4Sol_30.gif)
| > |
This shows that the given set is linearly independent.
The Invertible Matrix Theorem says that the matrix
with these columns is invertible, so the columns
span ![]() as well. Hence, they give a basis for
as well. Hence, they give a basis for ![]()
26. The pivot columns are columns 1,2,4. Hence
(by Theorem 13 in this section), columns 1,2,4
of A are a basis for Col(A):
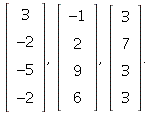
To find a basis for Nul(A), continue and put the
augmented matrix for Ax = 0 in rref:
| > |
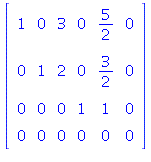
The parametrization of the set of solutions is determined by the
free variables ![]()
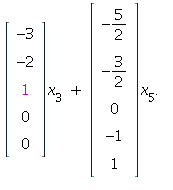 The two vectors here are a basis for Nul(A).
The two vectors here are a basis for Nul(A).
32. It is not all of ![]() by equivalence of parts d and h of the
by equivalence of parts d and h of the
Invertible Matrix Theorem).
34. The solution of Px = b is unique for all b ![]()
by the equivalence of parts d, f, g of the Invertible
Matrix Theorem.
Section 2.9.
6. This just means to find the scalars ![]() such
such
that ![]()
| > |
![table( [( 1, 3 ) = -5/2, ( 1, 2 ) = 0, ( 1, 1 ) = 1, ( 2, 3 ) = 1/2, ( 2, 1 ) = 0, ( 3, 1 ) = 0, ( 3, 2 ) = 0, ( 2, 2 ) = 1, ( 3, 3 ) = 0 ] )](images/PS4Sol_44.gif)
We see ![]() and
and ![]()
10. This is similar to number 26 from Section 2.8. A basis
for the column space consists of the pivot columns of
A -- columns 1,2,4. So dim Col(A) = 3. Then
dim Nul(A) = 2 (the number of free variables). Basis
for Nul(A):
| > |
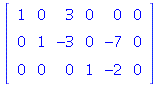
, Vector[column](%id = 140114252)](images/PS4Sol_49.gif) (from parametrization of set of solutions of homogeneous system).
(from parametrization of set of solutions of homogeneous system).
16. No. Col(A) cannot equal ![]() , since the columns are vectors with
, since the columns are vectors with
four components. The column space is a three-dimensional
subspace of ![]() The dimension of Nul(A) is the number of
The dimension of Nul(A) is the number of
free variables in the system. Since there are 3 pivot columns
out of 7 columns all together, there must be 4 free variables,
so dim Nul(A) = 4.
20. dim Nul(A) = 3 means there are 3 free variables.
In a 4 x 5 matrix, that leaves 2 pivot columns, and two
basis vectors for the column space. The rank
is the dimension of the column space, so rank(A) = 2.
22. If dim Span(![]() let {
let {![]()
be a basis for that subspace. Each ![]() can be written as a linear
can be written as a linear
combination of the basis vectors, so
![]()
![]()
...
![]()
Consider a linear combination of the ![]() that adds up to the
that adds up to the
zero vector:
![]()
substitute the above expressions, and collect
the terms involving each of the ![]()
![]()
Since the ![]() are linearly independent, this says
are linearly independent, this says
0 = ![]()
0 = ![]()
0 = ![]()
0 = ![]()
This is a homogeneous system of 4 linear equations in 5 variables
(the ![]()
variables than equations. Hence there is a nontrivial solution, and
the ![]() are linearly dependent.
are linearly dependent.
24. Rank = 1 means that the columns span a one-dimensional
space. Each column is a scalar multiple of one of them. Anything like
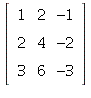 gives an example.
gives an example.
| > |