>

 

MATH 244 -- Linear Algebra 

Problem Set 2 Solutions 

February 2, 2007 

1.4/15  Form the augmented matrix [A|b] and perform the row 

operation The result is the matrix: 

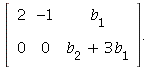 This implies that the system is consistent 

only when This is not true for every vector b, 

of course.  It is not true for instance if b = 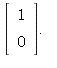Then  

The set of all b with is a line through the origin in 

18.  The two questions asked in this problem are two different  

ways of asking the same thing.  The span of the columns of B 

is all of exactly when the system  has a solution for  

all vectors  (look at highlighted statement at the bottom 

of page 42 in the text)  To answer the questions we proceed as 

in 15 above (but omitting the ``extended column'' for simplicity): 

>

 

>

 

>

 

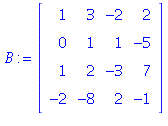
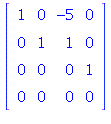
Note that the last row does not contain a pivot entry.  This means 

that the system will be inconsistent for some  choices of  y . 

In other words, there will be some equation that the components 

of  y  must satisfy:  constants) 

in order for a solution of  to exist.  So the answers are: 

No, the columns of B do not span   

No, the system does not have a solution for every y. 

26.  since   

31.  If A is 3 x 2, then there can be at most pivot columns. 

This means that the last row will not contain a pivot entry 

So the rref of A will contain a zero row.  As in 15, 18 above, 

this means that the system  will be inconsistent for 

some vectors  b.   The same reasoning shows that if  A 

is  m x n with  m > n,  then there are at most n pivot columns, 

which means some row cannot contain a pivot.  Hence in 

the rref of  A, there is at least one zero row, and the system  

will be inconsistent for some  b.   

32.  The answer is:  No.  Let be the three vectors, 

and let  A  be the 4 x 3  matrix with those columns.  Since 

4 > 3,  the previous exercise shows that   A x = y 

will be inconsistent for some y.  Hence by the highlighted 

statement at the bottom of page 42 in the text, there will 

be some vectors y  that are not in the span of the columns 

of A.  The corresponding general statement is:   

If we have n vectors in and  m > n, then those vectors 

do not span  

33.  To get a unique solution of the system Ax = b 

for some b,  A  must have three pivot entries, so 

the rref is  

1.5/6.  The rref of the augmented matrix is 

>

 

>

 

>

 

Hence the set of all solutions in parametric form is 

(set the free variable   

7.  Proceed as in 6: 

>

 

>

 

>

 

Here are free variables.  With  

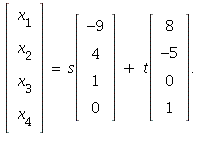
16.  The coefficient matrix here is the same as in problem 6.  Hence 

we can apply Theorem 6 from page 53 in the text and save some  

work, provided we can find a particular solution p.  By inspection 

is one solution of the system.  Hence Theorem 6 says 

the set of all solutions of the system will be 

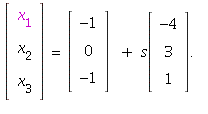This is the parametrization of  

a line in parallel to the line from problem 6. 

(Note: if you compute the solution by reducing the inhomogeneous  

augmented matrix to echelon form, you will find a different particular  

solution: 

p =  

Theorem 6 works with any particular solution, though.  You just  

get different parametrizations of the same line.   

36.  Any matrix whose rows dot with the given vector to give 0 

is OK.  One "random" example is 

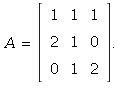
37.  To find a suitable matrix  A,  just proceed as in 36.   

One "random" matrix that works is 

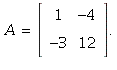
The set of solutions of  A x = 0  is spanned by  

Start with a general vector  b  and form the augmented matrix: 

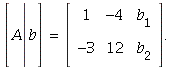
Then if we replace row 2 by row 2 plus 3 times row 1 we get: 

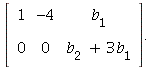
If  then the system is inconsistent.  Take  

b = for instance.  We get an inconsistent system A x = b, 

so the set of solutions for this is the empty set.  The empty  

set is certainly not a line in parallel to the line through 

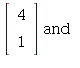the origin (the set of solutions of  A x = 0).   

This does not contradict Theorem 6 because that result 

includes the hypothesis that the inhomogeneous system 

Ax = b  is consistent.  The theorem does not apply with our  b.   

38.  No, there does not exist such a matrix.  One way to see this: 

when row operations are applied to the augmented matrix [A|y]  

there must be at least one row of the form [0 0 0 | *]  with * ≠ 0.   

Now apply the same row operations to the augmented matrix 

[A|z].  Then the entries in the 4th column in the zero row or rows 

must now be zero since the system is consistent.  But that means 

that the system [A|z] has at least one free variable, so the  

solution is not unique.   (A second way to prove this is to  

note that if [A|z] gives a unique solution for any z, then 

A must have three pivot columns, and the same will then 

be true for [A|y], since you would do the same row operations 

on that system.) 

1.7/1.  Determining whether a given set of vectors is 

linearly dependent is the same as determining whether 

the homogeneous system [A | 0 ]  (A = matrix whose  

columns are the given vectors) has any free variables. 

If so, then there is a way to make a linear combination 

of the columns sum to zero with some coefficients 

nonzero, and the set is dependent.  If not, then there  

there is no such linear combination, and the set is 

independent.   

>

 

>

 

>

 

No free variables, so the vectors are linearly independent. 

6.   

>

 

>

 

>

 

No free variables, so linearly independent. 

9.  If you are observant, you can answer this one with 

no calculations whatsoever!   

a)  The span W of is a line in  because  

The vector  cannot be on that line 

(whatever h happens to be) because is not a scalar  

multiple of (the first two components are "wrong":   

-7 ≠(-3)(5)) So:  no h -- is never in W. 

b)  The set is linearly dependent for 

all h ∈ ℝ  because of the equation  

32.  is one nontrivial solution (any scalar multiple 

of this vector is another).   

General Fact:  Any set of vectors containing a linearly  

dependent subset is linearly dependent. 

34.  This is true because we can make the linear dependence 

relation 

(Note the coefficient of so this implies linear dependence. 

36.  This is false because there could be some other 

dependence between the vectors that does not 

involve  

set by problem 34.) 

38.  This is true.    Here is a proof.  Consider any equation 

We can add a term with a zero  

coefficient on the left without changing anything: 

But now we are assuming that the set of 4 vectors is linearly 

independent.  That means that in this linear combination 

that adds up to the zero vector, all the coefficients must  

be zero:  That shows that  

satisfies the definition of linear independence.   

General Fact:  Any subset of a linearly independent set is 

linearly independent. 

(The general proof follows exactly the same reasoning as 

for this special case.)