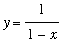MATH 134 -- Intensive Calculus for Science

April 3, 2002

Geometric series and polynomial approximations.

Our formula for the sum of an infinite geometric series

shows that if then

+ ... =

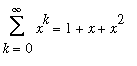If we stop the summation after a finite number of terms,

the result is a polynomial that can be thought of as a

simple polynomial approximating function for the (more)

complicated rational function 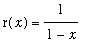. Here are some

graphs showing how this works. First the polynomial 1 + x

and r( x ) -- the rational function has a vertical asymptote

at x = 1, so we "cut it off before then":

> plot({1+x,1/(1-x)},x = -1..0.9,color=blue);

Now add one more term into the polynomial --

> plot({1+x+x^2,1/(1-x)},x = -1..0.9,color=blue);

One more term --

> plot({1+x+x^2+x^3,1/(1-x)},x = -1..0.9,color=blue);

One more --

> plot({1+x+x^2+x^3+x^4,1/(1-x)},x = -1..0.9,color=blue);

As we increase the degree of the polynomial, note how its graph is getting closer to

the graph