MATH 134 -- Intensive Calculus For Science 2

Comments on Lab Day 2, Question 6

The Taylor polynomials for the function with

approximate the function well inside the interval -1 < x < 1,

but not outside that interval. This can be seen by plotting

on different ranges of x values, as follows:

> restart;

> f := ln(x+1);

For example, consider the 16th degree polynomial

> p16:=convert(taylor(f,x=0,17),polynom);

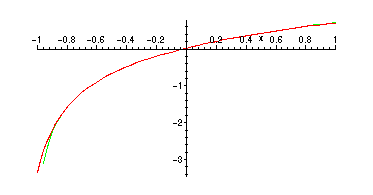
On the interval -1 < x < 1, the graphs of f and are nearly indistinguishable:

> plot({f,p16},x=-1..1);

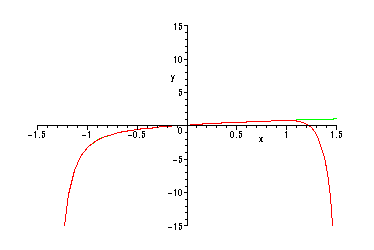
However, on the larger interval -1.5 < x < 1.5, the graphs look quite different (look at

the points with x > 1):

> plot({f,p16},x=-1.5..1.5,y=-15..15);

>

So, the interval where the Taylor polynomials give a good approximation to f

does not keep growing to arbitrary size .

The reason for this (in this example) is that the domain of the function

is the set of real x > - 1. The graph actually has a vertical asymptote

at x = - 1. It is a general property of Taylor series that if a function has a vertical

asymptote at x = b, then the radius of convergence of the Taylor series expanded at

x = a cannot be larger than . Here so the radius of

convergence is no bigger than . This is why the interval cannot

be larger than -1 < x < 1.