MATH 174 -- Applied Mathematics 2

April 25, 2000

Modulation and Demodulation Techniques

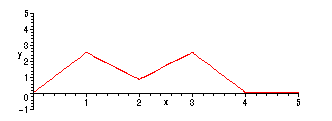
We begin with a piecewise-linear, time-limited signal f with f(x) >= 0 all x:

> restart;

> f := x->piecewise(0 < x and x < 1,5*x/2,1 < x and x < 2,25/6-5*x/3,2 < x and x < 3, -5/2 + 5*x/3 ,3 < x and x < 4,10 - 5*x/2);

> plot(f(x),x=0..5,y=-1..5);

The Fourier transform of f (OK to use the analog formulas rather than FFT here since f is relatively

simple!!):

> FTRf := omega->evalf(int(f(x)*cos(omega*x),x=0..4));

> FTIf := omega->evalf(int(f(x)*sin(omega*x),x=0..4));

> FPSf := omega->sqrt(FTRf(omega)^2+FTIf(omega)^2);

> plot(FPSf(omega),omega=-50..50,numpoints=200);

>

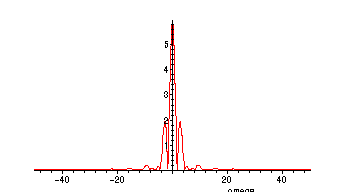
Double Side-band (DSB) Modulation

Using DSB amplitude modulation, we would transmit the product of f and a "carrier signal"

, where is relatively large (ideally, we would want this so large that

the Fourier transform of f was zero outside [ ]).

Note: This is very close to zero for | | > 30, so we will take that as our carrier frequency.

After modulation:

> g := x -> cos(30*x)*f(x);

Note that the outline of the signal f is visible in the "envelope" of the modulated signal g:

> gp:=plot(g(x),x=0..5,color=red):

> fp:=plot(f(x),x=0..5,color=black):

> with(plots): display({fp,gp});

>

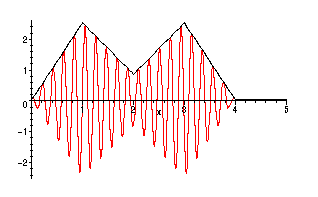
Fourier Transform of the Modulated Signal

The Fourier transform of the modulated signal g consists of two shifted and scaled

copies of the transform of f, superposed on each other (i.e. added). The shifting

left and right is by the amount = 30:

> FTRg := omega->evalf(int(g(x)*cos(omega*x),x=0..4));

> FTIg := omega->evalf(int(g(x)*sin(omega*x),x=0..4));

> FPSg := omega->sqrt(FTRg(omega)^2+FTIg(omega)^2);

> plot(FPSg(omega),omega=-50..50,numpoints=200);

>

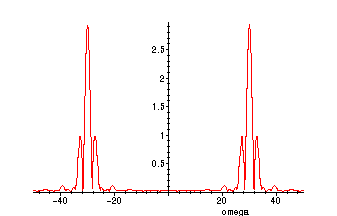
Synchronous Demodulation

At the other end of the transmission channel, to recover the original signal, we

can use synchronous demodulation:

a) Multiply g(x) by another factor of

> h:=x -> g(x)*cos(30*x);

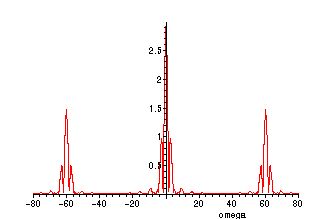
The Fourier transform of this new function h(x) now consists of three superposed copies of the

transform of f:

> FTRh := omega->evalf(int(h(x)*cos(omega*x),x=0..4));

> FTIh := omega->evalf(int(h(x)*sin(omega*x),x=0..4));

> FPSh := omega->sqrt(FTRh(omega)^2+FTIh(omega)^2);

> plot(FPSh(omega),omega=-80..80,numpoints=300);

>

Question: How can we recover f(x) from this information?

We can recover f(x) (up to a good approximation) by:

1) Putting h(x) through a low-pass filter (retaining only frequencies

in the range -30 to 30, for example)

2) Amplifying the resulting signal (multiplying by 2)

>

Quadrature Amplitude Modulation (QAM)

This is a method for increasing the amount of information that can be transmitted via

a modem and a communications channel. The idea is that two signals can be sent

simultaneously, since the above DSB approach essentially only uses real parts of the

signal and its Fourier Transform. Suppose we wanted to send the signal f(x) above,

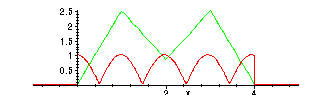
and a second signal g(x):

> g := x -> piecewise(0<=x and x<=4, abs(cos(3.2*x)),0);

> plot({f(x),g(x)},x=-1..5);

For QAM, we transmit the signal

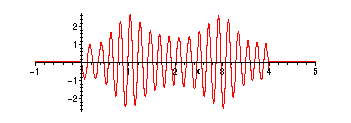
> send := x->cos(30*x)*f(x) - sin(30*x)*g(x):

> plot(send(x),x=-1..5);

To demodulate at the other end of the transmission channel, we proceed as follows. First

we multiply by .

> F1:=x->cos(30*x)*send(x);

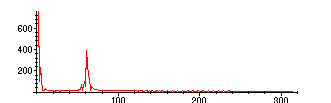
The Fourier Transform of this looks like this. (We use FFT here instead of the integral

formula for the FT):

> readlib(FFT);

> samplesR:=array([seq(evalf(F1(4*j/1024)),j=0..1023)]):

> samplesI:=array([seq(0,j=0..1023)]):

> FFT(10,samplesR,samplesI);

> FFTpoints:=[seq([2*Pi*k/4,sqrt(samplesR[k]^2+samplesI[k]^2)],k=1..200)]:

> plot(FFTpoints);

If we low-pass filter this (pass band ), and amplify, we recover f:

> filterR:=[seq(1,j=1..20),seq(0,j=21..1003),seq(1,j=1004..1024)]:

> filterI:=[seq(0,j=1..1024)]:

> FsamplesR:=array([seq(samplesR[j]*filterR[j],j=1..1024)]):

> FsamplesI:=array([seq(samplesI[j]*filterR[j],j=1..1024)]):

> iFFT(10,FsamplesR,FsamplesI);

> points:=[seq([4*j/1024,2*FsamplesR[j]],j=1..1024)]:

> plot(points);

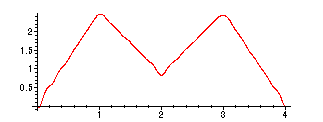
Similarly, we recover g(x) by multiplying by and proceeding as above:

>

> F2:=x->sin(30*x)*send(x);

The Fourier Transform of this looks like this. (We use FFT here instead of the integral

formula for the FT):

> samplesR:=array([seq(evalf(F2(4*j/1024)),j=0..1023)]):

> samplesI:=array([seq(0,j=0..1023)]):

> FFT(10,samplesR,samplesI);

> FFTpoints:=[seq([2*Pi*k/4,sqrt(samplesR[k]^2+samplesI[k]^2)],k=1..200)]:

> plot(FFTpoints);

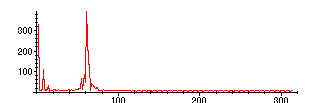
If we low-pass filter this (pass band ), and multiply by -2, we recover g (approximately)

> filterR:=[seq(1,j=1..20),seq(0,j=21..1003),seq(1,j=1004..1024)]:

> filterI:=[seq(0,j=1..1024)]:

> FsamplesR:=array([seq(samplesR[j]*filterR[j],j=1..1024)]):

> FsamplesI:=array([seq(samplesI[j]*filterR[j],j=1..1024)]):

> iFFT(10,FsamplesR,FsamplesI);

> points:=[seq([4*j/1024,-2*FsamplesR[j]],j=1..1024)]:

> plot(points);

>

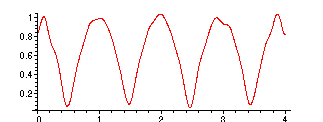
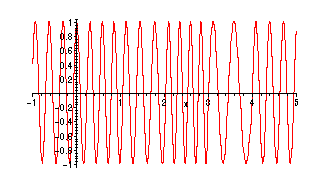
Frequency Modulation (FM)

Comment: The other commonly-used method for radio transmissions

is frequency modulation (FM). A corresponding FM signal for f:

> plot(cos((20+f(x))*x),x=-1..5,numpoints=100);

>