Mathematics 36, section 5 -- AP Calculus
Discussion 3 -- Total Change of a function, or
A Balloon Trip with the Montgolfier Brothers
October 6, 1999
Goals
We have now reached the end of the section of the course devoted to
Taylor polynomials and series. As a foretaste of what comes next,
today, we will consider the relationship between
the rate of change of a function, and the total change
of the function over some interval of independent variable values.
The Story
The Montgolfier brothers, Joseph and Etienne, were pioneers in
hot-air ballooning in the late 1700's in France. If they had possessed
appropriate instruments, they might have left a record of one
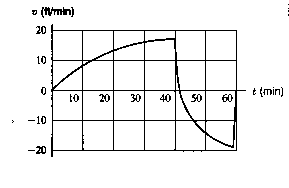
of their early experiments as shown in the graph below. The graph
shows the vertical velocity v of their balloon as
a function of time t. (This means v = dy/dt,
the rate of change of the height of the balloon, as a function of t, positive
values for v mean the balloon is going up; negative values, down.
Their acceleration at time t is a = dv/dt =
d2 y/dt2.)
Discussion Questions
- Over what intervals was the acceleration positive,
negative. Was it ever zero? What happened at t = 40?
(Think about how a hot-air balloon works.)
- At what time was the greatest altitude, y
achieved? (Be careful!) Call that time t = a.
- Next, let's try to estimate the
greatest altitude -- the total change in y over the interval
t = 0 to t = a. For instance, what would happen
if you subdivided the interval of t-values [0,a] into
n equal smaller
periods
0 < t1 < t2 < ... < tn-1 <
tn = a and "sampled" the v(t) function at the start
of each interval. Explain why the total distance traveled over
the kth interval is approximately
v(tk-1) Delta t, k = 1, ... , n.
Use this to get an estimate of the total distance
traveled over the whole interval. (Give both a numerical value
and a general formula or recipe for what you are doing.)
- What happened at the end of this flight? Did the balloon
end up at the top of a hill, in a valley, or at the same
height it started? How can you tell?
Assignment
Group write-ups due in class no later than Friday, October 15.

