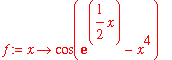
MATH 136, Section 4

Solutions for Lab 1 (Lab Activity 2)

September 17, 2003

A. 1)

>	f:=x->cos(exp(x/2)-x^4);

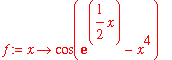
>	plot(f(x),x=-2..2);

2.  To study whether  f(x)   is differentiable at   x = - 1, we look at the difference

quotient 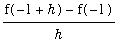       and let   h -> 0.   To see that limit, we plot

the difference quotient as a function of   h   and ``zoom in'' toward   h = 0:

>	plot((f(-1+h) - f(-1))/h,h=-0.1..0.1);

>	plot((f(-1+h) - f(-1))/h,h=-0.001..0.001);

3. Because the   y - coordinate  seems to be approaching about 1.65 as   h -> 0 , we estimate

f '(-1) = 1.65  (approx.)

4.  Now we plot   y = f(x)  and the tangent line together:

>	plot([f(x),f(-1)+1.65*(x+1)],x=-2..0);

Zooming in toward x = -1:

>	plot([f(x),f(-1)+1.65*(x+1)],x=-1.1..-0.9);

>	plot([f(x),f(-1)+1.65*(x+1)],x=-1.001..-0.999);

Note that as the x- range gets smaller, it gets harder and harder to distinguish

between the graph of   f   and the tangent line.  One way to say this is that

the graph  y = f(x)  is very close to  a straight  line  with slope f'(-1)  for

x near -1.  Or equivalently, the slope of the graph  y = f(x)  is very close

f ' (-1) approx = 1.65  near  x = -1.

B.  1.

>	g:=x->abs(x-2)^(1/5)*cos(x^2);

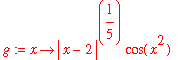
>	plot(g(x),x=1..3);

To investigate whether   g'(2)   exists, we can again plot the difference quotient

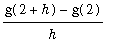  and zoom in toward  h  = 0:

>	plot((g(2+h)-g(2))/h,h=-0.1..0.1);

We get a graph that appears to have a vertical asymptote at   h  = 0.  No

amount of zooming toward  h = 0  can make that go away.  So

this suggests that   g'(2) does not exist because

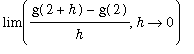
does not exist.

2.  We zoom in toward   x = 2 on the graph of  g  now:

>	plot(g(x),x=1.9..2.1);

>	plot(g(x),x=1.99..2.01);

Note that we are getting a sharp point on the graph here, a ``cusp''.

C)  In A, the limit of the difference quotient for the derivative

of   f   at   x = -1   did exist (equaled 1.65 approximately), so

f   was differentiable at   x = -1.   On the other hand

g'(2) did not exist from the graphical evidence.   A function is

differentiable at   x = a  if,  when we zoom in toward  x = a,

the graph  y = f(x)  gets closer and closer to the graph

of a linear function (the linear function whose graph is

the tangent line).