MATH 136 -- AP Calculus

October 17, 2003

An example of constructing (an approximation to) an antiderivative

of a function via the 2nd part of the Fundamental Theorem of Calculus.

The function  f:

>	f:=t->sin(1/t);

This is one case where no "obvious" antiderivative exists.  Indeed,

none of the methods we will discuss over the next few weeks of the class

will produce one either, because there is no elementary antiderivative!

However, if we define a new function  G  by approximating

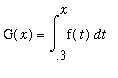  by a right-hand Riemann sum with n = 1000,

then     is giving us an approximate antiderivative of  f:

>	G:=x->add(f(0.3+i*(x-0.3)/1000)*(x-0.3)/1000,i=1..1000);

>	plot([f(x),G(x)],x=0.3..1.7,color=[red,blue],axes=boxed);

>

How do we interpret this?  The function that looks like it is always increasing is  G

(there is actually a very small interval starting at 0.3 on which G is decreasing,

but it increases almost immediately after that).   The other graph with the local

maximum is the graph of  f.    The function f  gives the slope of the graph of G.   Note

that the graph of  G  is clearly concave up for a while, then has an inflection point

at about   x = 0.7.    The point of inflection of G  (maximum positive slope of  G) occurs

at the local maximum of  f.  After that, the slope of  G  decreases but is still

positive.